TerraLiner:12 m Globally Mobile Beach House/Class-A Crossover w 6x6 Hybrid Drivetrain
- Thread starter biotect
- Start date
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
Most importantly, getting up to Monarch Pass is a long, extended slog. According to Google Maps, the distance from Cañon City, Colorado to Monarch Pass is 79.9 miles or 128.6 km, should take 1 hour and 38 minutes, and the elevation rises from from 1,625 m to 3448 m, for a total vertical rise of 1,823 m. This works out to a 1.4 % incline averaged over the whole distance – see https://en.wikipedia.org/wiki/Cañon_City,_Colorado and https://www.google.co.uk/maps/dir/C...416da48ac2ca0!2m2!1d-106.3255801!2d38.4966636 . Note that Google maps seems to assume an average speed of roughly 78.74 kph. However, much closer to the pass, from Poncha Springs, Colorado, the climb is considerably more steep – see https://www.google.co.uk/maps/dir/P...416da48ac2ca0!2m2!1d-106.3255801!2d38.4966636 . According to Google Maps, Poncha Springs to Monarch Pass is 18.2 miles or 29.3 km, should take 24 minutes, and the elevation rises from 2,275 m to 3448 m, for a total vertical rise of 1,173 m. This works out to a 4 % incline averaged over the whole distance – see https://en.wikipedia.org/wiki/Poncha_Springs,_Colorado . Here, Google seems to be assuming an average speed of 73 kph.
I didn’t bother calculating the route from Pueblo Colorado, because the elevation there, at 1,430 m, only about 200 m less than Cañon City – see https://en.wikipedia.org/wiki/Pueblo,_Colorado . The difference between La Junta and Pueblo is roughly the same: La Junta has an elevation of 1,243 m, about 200 m less than Pueblo – see https://en.wikipedia.org/wiki/La_Junta,_Colorado . So it seems clear that the Route 50's slope increases only gradually between La Junta and Cañon City; more again between Cañon City and Poncha Springs; and then very dramatically between Poncha Springs and Monarch Pass.
By way of contrast, the I -70 departs Denver at about 1,700 m, and reaches a peak altitude of 3,401 m inside the Eisenhower tunnel, for a total vertical travel of 1,670 m, almost the same as the vertical travel necessary to reach Monarch Pass. But the I-70 accomplishes this over a distance of just 46 miles, or 74 km, with an average grade of 2.2 % -- see https://www.google.co.uk/maps/dir/T...266aa577c950ef!2m2!1d-105.9056878!2d39.679042 , https://en.wikipedia.org/wiki/Eisenhower_Tunnel , and https://en.wikipedia.org/wiki/Denver . In one sense this makes the Eisenhower pass more interesting than the Monarch pass, because it's much steeper. But in another sense it's less interesting, because the travel time is much shorter, according to Google Maps, just 47 minutes. Here Google seems to assume a speed of roughly 95 kph.
The travel time on the Route 50 from Cañon City to Monarch Pass is therefore about double, and this interests me, because it's all uphill. When we factor in both drag from air-resistance + working against gravity to make the ascent, 1 hours and 40 minutes is a long time, a substantial period of constant battery drain, with no flats to interrupt and allow recharging. Whereas a short sharp ascent won't be combined with such a long period of air-resistance. So my guess is that the Monarch Pass will prove more challenging than the Eisenhower pass, from a power-demand point of view. I will test this intuition further along.
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
Most importantly, getting up to Monarch Pass is a long, extended slog. According to Google Maps, the distance from Cañon City, Colorado to Monarch Pass is 79.9 miles or 128.6 km, should take 1 hour and 38 minutes, and the elevation rises from from 1,625 m to 3448 m, for a total vertical rise of 1,823 m. This works out to a 1.4 % incline averaged over the whole distance – see https://en.wikipedia.org/wiki/Cañon_City,_Colorado and https://www.google.co.uk/maps/dir/C...416da48ac2ca0!2m2!1d-106.3255801!2d38.4966636 . Note that Google maps seems to assume an average speed of roughly 78.74 kph. However, much closer to the pass, from Poncha Springs, Colorado, the climb is considerably more steep – see https://www.google.co.uk/maps/dir/P...416da48ac2ca0!2m2!1d-106.3255801!2d38.4966636 . According to Google Maps, Poncha Springs to Monarch Pass is 18.2 miles or 29.3 km, should take 24 minutes, and the elevation rises from 2,275 m to 3448 m, for a total vertical rise of 1,173 m. This works out to a 4 % incline averaged over the whole distance – see https://en.wikipedia.org/wiki/Poncha_Springs,_Colorado . Here, Google seems to be assuming an average speed of 73 kph.
I didn’t bother calculating the route from Pueblo Colorado, because the elevation there, at 1,430 m, only about 200 m less than Cañon City – see https://en.wikipedia.org/wiki/Pueblo,_Colorado . The difference between La Junta and Pueblo is roughly the same: La Junta has an elevation of 1,243 m, about 200 m less than Pueblo – see https://en.wikipedia.org/wiki/La_Junta,_Colorado . So it seems clear that the Route 50's slope increases only gradually between La Junta and Cañon City; more again between Cañon City and Poncha Springs; and then very dramatically between Poncha Springs and Monarch Pass.
By way of contrast, the I -70 departs Denver at about 1,700 m, and reaches a peak altitude of 3,401 m inside the Eisenhower tunnel, for a total vertical travel of 1,670 m, almost the same as the vertical travel necessary to reach Monarch Pass. But the I-70 accomplishes this over a distance of just 46 miles, or 74 km, with an average grade of 2.2 % -- see https://www.google.co.uk/maps/dir/T...266aa577c950ef!2m2!1d-105.9056878!2d39.679042 , https://en.wikipedia.org/wiki/Eisenhower_Tunnel , and https://en.wikipedia.org/wiki/Denver . In one sense this makes the Eisenhower pass more interesting than the Monarch pass, because it's much steeper. But in another sense it's less interesting, because the travel time is much shorter, according to Google Maps, just 47 minutes. Here Google seems to assume a speed of roughly 95 kph.
The travel time on the Route 50 from Cañon City to Monarch Pass is therefore about double, and this interests me, because it's all uphill. When we factor in both drag from air-resistance + working against gravity to make the ascent, 1 hours and 40 minutes is a long time, a substantial period of constant battery drain, with no flats to interrupt and allow recharging. Whereas a short sharp ascent won't be combined with such a long period of air-resistance. So my guess is that the Monarch Pass will prove more challenging than the Eisenhower pass, from a power-demand point of view. I will test this intuition further along.
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
Here are some good videos of Monarch pass. The last second-to-last-two show the set where Fast & Furious 7 filmed at Monarch Pass; and the last video shows the result:
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
Here are some good videos of Monarch pass. The last second-to-last-two show the set where Fast & Furious 7 filmed at Monarch Pass; and the last video shows the result:
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
4. Iain's Equations
**************************************************
Here is a small recap of Iain's equations to calculate power, and how they are used.
To calculate the total amount of Force required, we add Froll + Fslope + Fair, to get a figure called "Ftotal", expressed in Newtons as kg m/s[SUP]2 [/SUP], a unit of Force -- see https://en.wikipedia.org/wiki/Newton_(unit) . To then obtain a figure for Watts, we multiple the figure in Newtons by the velocity in the scenario being considered. This gives us a final figure expressed as kg m[SUP]2[/SUP]/s[SUP]3[/SUP], which is the same as one Watt. So a value like 200,000 kg m[SUP]2[/SUP]/s[SUP]3[/SUP], is 200 KW.
**************************************************
(A) ..First we calculate Froll, the amount of Force required to keep a vehicle like the TerraLiner rolling in a theoretical vacuum. The equation here is Froll = cr m g .
cr = coefficient of rolling resistance. Rolling resistance can vary a lot, and this seems to depend significantly on tires -- see page 14, at http://ec.europa.eu/transport/modes/...shop_jrc_2.pdf .
I used the following table and articles to assume a coefficient of rolling resistance for the TerraLiner of 0.1 %, or 0.010 -- see http://www.engineeringtoolbox.com/ro...ce-d_1303.html , https://www.physicsforums.com/thread...trucks.603149/ , and https://www.physicsforums.com/thread...rucks.603149/:
m = the total mass of the TerraLiner + trailer, or 32,000 kg, the projected weight of the TerraLiner
g = gravitational acceleration, which is conventionally understood as 9.81 meters/seconds[SUP]2 [/SUP]at sea level -- see https://en.wikipedia.org/wiki/Gravitational_acceleration .
So Froll for the Terraliner = 0.010 x 32,000 kg x 9.81 m/s[SUP]2 [/SUP]= 3139.2 kg m/s[SUP]2 [/SUP]
Once we've calculated Froll once, we don't need to calculate it again, because the TerraLiner's weight is pretty much fixed, at least for now, for the purposes of this power-calculation exercise.
**************************************************
(B) ..Next we calculate Fslope, the amount of Force required to move a mass like the TerraLIner up a hill. Fslope = s m g
I. From Cañon City to Monarch Pass:
s = upward slope: 1.4 % = 0.014
m = total mass of the TerraLiner truck + trailer = 32,000 kg
g = 9.81 meters/seconds[SUP]2[/SUP]
Fslope = 0.014 x 32,000 kg x 9.81 m/s[SUP]2 [/SUP]= 4,394.9 kg m/s[SUP]2 [/SUP]
II. From Poncha Springs to Monarch Pass:
s = upward slope: 4 % = 0.04
m = total mass of truck and trailer = 32,000 kg
g = 9.81 meters/seconds[SUP]2[/SUP]
Fslope = 0.04 x 32,000 kg x 9.81 m/s[SUP]2 [/SUP]= 12,556.8 kg m/s[SUP]2 [/SUP]
Here we only need two "real world" calculations, one from Cañon City, and the other from Poncha Springs. But in addition, I will be exploring a more hypothetical scenario, in which the TerraLiner climbs an extended slope also 128.6 km, but 3 % the whole way, from sea-level to 3,858 m. In this hypothetical scenario:
III. From Sea Level to Monarch Pass:
s = upward slope: 3 % = 0.03
m = total mass of truck and trailer = 32,000 kg
g = 9.81 meters/seconds[SUP]2[/SUP]
Fslope = 0.03 x 32,000 kg x 9.81 m/s[SUP]2 [/SUP]= 9,417.6 kg m/s[SUP]2 [/SUP]
**************************************************
(C) ..Finally we calculate Fair, the amount of Force required to move the TerraLiner forward, overcoming air-resistance. This will be a combination of the speed the TerraLiner is traveling, + any headwind.
Fair = (r cd A v (speed + headwind wind)[SUP] 2[/SUP])/2
r = 1.29 kg/m³, the the density of air at sea level. The density of air drops with altitude, and varies directly with air pressure:
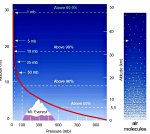
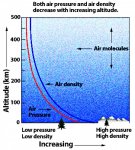
But we will just assume a sea-level air-density throughout. A bit more discussion in the next post.....
cd = 0.85, the drag coefficient. A typical truck/trailer is 0.96, a more streamlined bus is around 0.8, so I used 0.85 just to be conservative. But note that on one web-forum, a participant assumes a drag coefficient as good as 0.07 – see https://www.physicsforums.com/threads/rolling-resistance-for-large-trucks.603149/ , and also see https://en.wikipedia.org/wiki/Automobile_drag_coefficient .
A = 10 m[SUP]2 [/SUP], the projected frontal area. I just used the width x height, assuming that the TerraLiner will be 4 m tall x 2.50 m wide
v air = either 19 m/s, 25 m/s, 27.8 m/s, 30 m/s, or 32.8 m/s. This is the total of speed + any headwinds in m/s.
I decided to do calculations for three scenarios, one in which the TerraLiner takes on this slope at 50 kph with a moderate headwind, the second at 90 kph without and with headwind, and the third at 100 kph without and with headwind.
I. In the first 50 kph = 13.9 m/s, to which I added a moderate headwind of 18 kph, or 5 m/s, to arrive at 19 m/s.
II. In the second 90 kph = 25 m/s. When 5 m/s of headwind is added, this become 30 m/s.
III. In the third, 100 kph = 27.8 m/s, and when 5 m/s of headwind is added, this becomes 32.8 m/s.
So for instance, in the first scenario where the TerraLIner is traveling 50 kph against a moderate headwind of 18 kph, we obtain the following result:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (19 m/s)[SUP] 2[/SUP])/2 = 3,958.36 m/s[SUP]2 [/SUP]divided by 2 = 1979.18 kg m/s[SUP]2[/SUP]
**************************************************
Note that I've left out Faccel, the Force required for accelerations, for reasons already explained in the exchange with Iain -- see posts #1993 and #1994 at http://www.expeditionportal.com/for...igid-Torsion-Free-Frame?p=1964749#post1964749 . The power required to accelerate the TerraLiner at the beginning of the slope is a one-off, and the constant start/stop accelerations and decelerations en-route will presumably be handled well by the massive-hub-motor regenerative braking system. I've simply posited abstractly "perfect" energy recovery here, although of course in the real world it won't be that. But all physics equations are theoretical abstractions, and what we're after right now is merely rough-ballpark power requirement figures.
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
4. Iain's Equations
**************************************************
Here is a small recap of Iain's equations to calculate power, and how they are used.
To calculate the total amount of Force required, we add Froll + Fslope + Fair, to get a figure called "Ftotal", expressed in Newtons as kg m/s[SUP]2 [/SUP], a unit of Force -- see https://en.wikipedia.org/wiki/Newton_(unit) . To then obtain a figure for Watts, we multiple the figure in Newtons by the velocity in the scenario being considered. This gives us a final figure expressed as kg m[SUP]2[/SUP]/s[SUP]3[/SUP], which is the same as one Watt. So a value like 200,000 kg m[SUP]2[/SUP]/s[SUP]3[/SUP], is 200 KW.
**************************************************
(A) ..First we calculate Froll, the amount of Force required to keep a vehicle like the TerraLiner rolling in a theoretical vacuum. The equation here is Froll = cr m g .
cr = coefficient of rolling resistance. Rolling resistance can vary a lot, and this seems to depend significantly on tires -- see page 14, at http://ec.europa.eu/transport/modes/...shop_jrc_2.pdf .
I used the following table and articles to assume a coefficient of rolling resistance for the TerraLiner of 0.1 %, or 0.010 -- see http://www.engineeringtoolbox.com/ro...ce-d_1303.html , https://www.physicsforums.com/thread...trucks.603149/ , and https://www.physicsforums.com/thread...rucks.603149/:
m = the total mass of the TerraLiner + trailer, or 32,000 kg, the projected weight of the TerraLiner
g = gravitational acceleration, which is conventionally understood as 9.81 meters/seconds[SUP]2 [/SUP]at sea level -- see https://en.wikipedia.org/wiki/Gravitational_acceleration .
So Froll for the Terraliner = 0.010 x 32,000 kg x 9.81 m/s[SUP]2 [/SUP]= 3139.2 kg m/s[SUP]2 [/SUP]
Once we've calculated Froll once, we don't need to calculate it again, because the TerraLiner's weight is pretty much fixed, at least for now, for the purposes of this power-calculation exercise.
**************************************************
(B) ..Next we calculate Fslope, the amount of Force required to move a mass like the TerraLIner up a hill. Fslope = s m g
I. From Cañon City to Monarch Pass:
s = upward slope: 1.4 % = 0.014
m = total mass of the TerraLiner truck + trailer = 32,000 kg
g = 9.81 meters/seconds[SUP]2[/SUP]
Fslope = 0.014 x 32,000 kg x 9.81 m/s[SUP]2 [/SUP]= 4,394.9 kg m/s[SUP]2 [/SUP]
II. From Poncha Springs to Monarch Pass:
s = upward slope: 4 % = 0.04
m = total mass of truck and trailer = 32,000 kg
g = 9.81 meters/seconds[SUP]2[/SUP]
Fslope = 0.04 x 32,000 kg x 9.81 m/s[SUP]2 [/SUP]= 12,556.8 kg m/s[SUP]2 [/SUP]
Here we only need two "real world" calculations, one from Cañon City, and the other from Poncha Springs. But in addition, I will be exploring a more hypothetical scenario, in which the TerraLiner climbs an extended slope also 128.6 km, but 3 % the whole way, from sea-level to 3,858 m. In this hypothetical scenario:
III. From Sea Level to Monarch Pass:
s = upward slope: 3 % = 0.03
m = total mass of truck and trailer = 32,000 kg
g = 9.81 meters/seconds[SUP]2[/SUP]
Fslope = 0.03 x 32,000 kg x 9.81 m/s[SUP]2 [/SUP]= 9,417.6 kg m/s[SUP]2 [/SUP]
**************************************************
(C) ..Finally we calculate Fair, the amount of Force required to move the TerraLiner forward, overcoming air-resistance. This will be a combination of the speed the TerraLiner is traveling, + any headwind.
Fair = (r cd A v (speed + headwind wind)[SUP] 2[/SUP])/2
r = 1.29 kg/m³, the the density of air at sea level. The density of air drops with altitude, and varies directly with air pressure:
But we will just assume a sea-level air-density throughout. A bit more discussion in the next post.....
cd = 0.85, the drag coefficient. A typical truck/trailer is 0.96, a more streamlined bus is around 0.8, so I used 0.85 just to be conservative. But note that on one web-forum, a participant assumes a drag coefficient as good as 0.07 – see https://www.physicsforums.com/threads/rolling-resistance-for-large-trucks.603149/ , and also see https://en.wikipedia.org/wiki/Automobile_drag_coefficient .
A = 10 m[SUP]2 [/SUP], the projected frontal area. I just used the width x height, assuming that the TerraLiner will be 4 m tall x 2.50 m wide
v air = either 19 m/s, 25 m/s, 27.8 m/s, 30 m/s, or 32.8 m/s. This is the total of speed + any headwinds in m/s.
I decided to do calculations for three scenarios, one in which the TerraLiner takes on this slope at 50 kph with a moderate headwind, the second at 90 kph without and with headwind, and the third at 100 kph without and with headwind.
I. In the first 50 kph = 13.9 m/s, to which I added a moderate headwind of 18 kph, or 5 m/s, to arrive at 19 m/s.
II. In the second 90 kph = 25 m/s. When 5 m/s of headwind is added, this become 30 m/s.
III. In the third, 100 kph = 27.8 m/s, and when 5 m/s of headwind is added, this becomes 32.8 m/s.
So for instance, in the first scenario where the TerraLIner is traveling 50 kph against a moderate headwind of 18 kph, we obtain the following result:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (19 m/s)[SUP] 2[/SUP])/2 = 3,958.36 m/s[SUP]2 [/SUP]divided by 2 = 1979.18 kg m/s[SUP]2[/SUP]
**************************************************
Note that I've left out Faccel, the Force required for accelerations, for reasons already explained in the exchange with Iain -- see posts #1993 and #1994 at http://www.expeditionportal.com/for...igid-Torsion-Free-Frame?p=1964749#post1964749 . The power required to accelerate the TerraLiner at the beginning of the slope is a one-off, and the constant start/stop accelerations and decelerations en-route will presumably be handled well by the massive-hub-motor regenerative braking system. I've simply posited abstractly "perfect" energy recovery here, although of course in the real world it won't be that. But all physics equations are theoretical abstractions, and what we're after right now is merely rough-ballpark power requirement figures.
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
5. Cañon City to Monarch Pass, 1.4 % slope for 128.6 km, at 50 kph with moderate headwind of 18 kph
**************************************************
Now as Iain pointed out, the final figure has to be expressed in terms of kg m[SUP]2[/SUP]/s[SUP]3[/SUP], which is the definition of a 1 W of power – see https://en.wikipedia.org/wiki/SI_derived_unit . Multiplying FTotal by the velocity of the truck expressed in m/s has this effect, and incidentally, also means the velocity for air speed will end up cubed. When I did the calculations earlier for the drive up to Lake Tahoe, I only squared the velocity (i.e. raised it to the power of 2), because I merely added the F-values. This was a mistake. See http://www.expeditionportal.com/for...igid-Torsion-Free-Frame?p=1965033#post1965033 and https://strava.zendesk.com/entries/20959332-Power-Calculations .
In the 50 kph + moderate headwind scenario, we add the above figures for Froll + Fslope + Fair, to get FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 1979.18 m/s[SUP]2 [/SUP]= 9513.28 kg m/s[SUP]2 [/SUP]. Then multiplying this by the velocity, 50 kph, or 13.89 m/ps, we get 132,139.5 kg m[SUP]2[/SUP]/s[SUP]3[/SUP], or 132.1 KW per hour, to climb from Cañon City to Monarch Pass.
However, this figure assumes an artificial 100 % efficiency for a drive-train consisting of electric hub motors, so there is no 30 % efficiency-loss due to a traditional transmission. I am still waiting to hear from Haf-E as to what he thinks might be the efficiency loss for either an inter-axle transmission, or for Wrightspeed’s gearing on its hub motors, or both…… ...Haf-E, if you are reading this, please post! In the meantime, let’s suppose a 10 % loss of efficiency for hub motors, as suggested by Ian in post #1994 at http://www.expeditionportal.com/forum/threads/124789-Fully-Integrated-MAN-or-TATRA-6x6-or-8x8-Expedition-RV-w-Rigid-Torsion-Free-Frame?p=1965033#post1965033 . So dividing 132.1 W by 0.90, we arrive at a power figure of 146.8 KW per hour.
**************************************************
6. Double-Checking our Figures against On-Line Web Calculators:
http://ecomodder.com/forum/tool-aero-rolling-resistance.php
and
http://buggies.builtforfun.co.uk/Calculator/index.html
**************************************************
To ensure that we are more or less on the right track, let's compare this to the figures provides by some on-line calculators. There is one very good calculator at http://ecomodder.com/forum/tool-aero-rolling-resistance.php , which allows one to input diverse figures for vehicle weight, coefficient of rolling resistance, coefficient of drag, etc. It also provides a very interesting and useful list of possible air-density options:
So assuming 1.29 kg/m³ as a figure for air-density at sea level is a bit severe: this is air-density at seal level where the temperature is 0 C, or 32 F. During the summer and in warm climates air-density drops to 1.204 kg/m³ :
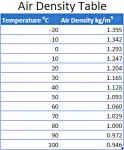
A number of places I've seen 1.225 quoted as the sea-level convention kg/m³, not 1.29 kg/m³. On the other hand, it's probably best to err on the conservative side when making our calculations, and so we'll stick with Iain's figure of 1.29. I just wanted to underscore how this is a conservative figure, not a liberal one. Air density also decreases significantly with altitude, but again we will err on the side of caution, and stick with 1.29 throughout.
So plugging our numbers into this calculator, for Froll + Fair (where "v" is 50 kph + an 18 kph headwind = 68 kph, or 19 m/s), we get a power consumption requirement of roughly 95,697.72 W , or 95.7 KW. The table does not provide an exact power figure for 68 kph, so I averaged the figures for 64 kph and 72 kph:
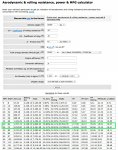
This web-calculator does not provide for Fslope, but let's check to see if our calculations for Froll + Fair were in roughly the right ballpark.
3,139.2 kg m/s[SUP]2 + [/SUP]1,979.18 m/s [SUP]2 = [/SUP]5,118.38 kg m/s[SUP]2[/SUP]. We multiple this by the TerraLiner's velocity of 50 kph, or 13.89 m/s, and we get 71,094.30 m[SUP]2[/SUP]/s[SUP]3[/SUP]. Then dividing by 0.9 for hub-gear inefficiency, we get 78,993.33 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 80 KW. So if anything, Iain's equations seem to be yielding numbers that are slightly low. In this case, about 16 KW per hour too low. But of course I still may not be using Iain's equations correctly.....
There is another web-calcuator at http://buggies.builtforfun.co.uk/Calculator/index.html, and this one includes Fslope. For a gradient slope of 1.4 %, one needs to input "72", because the calculator then interprets that as 1:72, or "1 in 72", which is roughly the same thing as 1.4 %. It's also the same thing as an angle of slope of 0.8 degrees:
Notice that here too I entered a "zero" value for acceleration. Above there are two calculations. The first is for a vehicle speed of 50 kph, and after taking into account drive-train inefficiency, this web-calculator produced a figure of 132 KW. The second is for a vehicle speed of 68 kph, which of course is slightly different than a vehicle speed of 50 kph + 18 kph for headwind. Even still, this calculator produced a final figure of 198.4 KW. The first figure is less than our calculated 146.8 KW per hour using Iain's formulas, but the second figure is significantly more, about 50 KW more. On the other hand, our Froll and Fair figures using Iain's formulas are only 16 KW lower per hour than those produced by the first web-calculator.
So at the very beginning, all of this should suggest that any calculations of possible TerraLiner power requirements should be taken with a grain of salt. These two web-calculators are not up-front about the formulas they use, so who knows what might account for the discrepancy in their computations. But the mere fact that I inserted identical values in both, and got somewhat divergent results, seems to suggest that both contain hidden assumptions that are skewing results one way or the other. As the second calculator warns:
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
5. Cañon City to Monarch Pass, 1.4 % slope for 128.6 km, at 50 kph with moderate headwind of 18 kph
**************************************************
Now as Iain pointed out, the final figure has to be expressed in terms of kg m[SUP]2[/SUP]/s[SUP]3[/SUP], which is the definition of a 1 W of power – see https://en.wikipedia.org/wiki/SI_derived_unit . Multiplying FTotal by the velocity of the truck expressed in m/s has this effect, and incidentally, also means the velocity for air speed will end up cubed. When I did the calculations earlier for the drive up to Lake Tahoe, I only squared the velocity (i.e. raised it to the power of 2), because I merely added the F-values. This was a mistake. See http://www.expeditionportal.com/for...igid-Torsion-Free-Frame?p=1965033#post1965033 and https://strava.zendesk.com/entries/20959332-Power-Calculations .
In the 50 kph + moderate headwind scenario, we add the above figures for Froll + Fslope + Fair, to get FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 1979.18 m/s[SUP]2 [/SUP]= 9513.28 kg m/s[SUP]2 [/SUP]. Then multiplying this by the velocity, 50 kph, or 13.89 m/ps, we get 132,139.5 kg m[SUP]2[/SUP]/s[SUP]3[/SUP], or 132.1 KW per hour, to climb from Cañon City to Monarch Pass.
However, this figure assumes an artificial 100 % efficiency for a drive-train consisting of electric hub motors, so there is no 30 % efficiency-loss due to a traditional transmission. I am still waiting to hear from Haf-E as to what he thinks might be the efficiency loss for either an inter-axle transmission, or for Wrightspeed’s gearing on its hub motors, or both……
...Haf-E, if you are reading this, please post! In the meantime, let’s suppose a 10 % loss of efficiency for hub motors, as suggested by Ian in post #1994 at http://www.expeditionportal.com/forum/threads/124789-Fully-Integrated-MAN-or-TATRA-6x6-or-8x8-Expedition-RV-w-Rigid-Torsion-Free-Frame?p=1965033#post1965033 . So dividing 132.1 W by 0.90, we arrive at a power figure of 146.8 KW per hour. **************************************************
6. Double-Checking our Figures against On-Line Web Calculators:
http://ecomodder.com/forum/tool-aero-rolling-resistance.php
and
http://buggies.builtforfun.co.uk/Calculator/index.html
**************************************************
To ensure that we are more or less on the right track, let's compare this to the figures provides by some on-line calculators. There is one very good calculator at http://ecomodder.com/forum/tool-aero-rolling-resistance.php , which allows one to input diverse figures for vehicle weight, coefficient of rolling resistance, coefficient of drag, etc. It also provides a very interesting and useful list of possible air-density options:
So assuming 1.29 kg/m³ as a figure for air-density at sea level is a bit severe: this is air-density at seal level where the temperature is 0 C, or 32 F. During the summer and in warm climates air-density drops to 1.204 kg/m³ :
A number of places I've seen 1.225 quoted as the sea-level convention kg/m³, not 1.29 kg/m³. On the other hand, it's probably best to err on the conservative side when making our calculations, and so we'll stick with Iain's figure of 1.29. I just wanted to underscore how this is a conservative figure, not a liberal one. Air density also decreases significantly with altitude, but again we will err on the side of caution, and stick with 1.29 throughout.
So plugging our numbers into this calculator, for Froll + Fair (where "v" is 50 kph + an 18 kph headwind = 68 kph, or 19 m/s), we get a power consumption requirement of roughly 95,697.72 W , or 95.7 KW. The table does not provide an exact power figure for 68 kph, so I averaged the figures for 64 kph and 72 kph:
This web-calculator does not provide for Fslope, but let's check to see if our calculations for Froll + Fair were in roughly the right ballpark.
3,139.2 kg m/s[SUP]2 + [/SUP]1,979.18 m/s [SUP]2 = [/SUP]5,118.38 kg m/s[SUP]2[/SUP]. We multiple this by the TerraLiner's velocity of 50 kph, or 13.89 m/s, and we get 71,094.30 m[SUP]2[/SUP]/s[SUP]3[/SUP]. Then dividing by 0.9 for hub-gear inefficiency, we get 78,993.33 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 80 KW. So if anything, Iain's equations seem to be yielding numbers that are slightly low. In this case, about 16 KW per hour too low. But of course I still may not be using Iain's equations correctly.....
There is another web-calcuator at http://buggies.builtforfun.co.uk/Calculator/index.html, and this one includes Fslope. For a gradient slope of 1.4 %, one needs to input "72", because the calculator then interprets that as 1:72, or "1 in 72", which is roughly the same thing as 1.4 %. It's also the same thing as an angle of slope of 0.8 degrees:
Notice that here too I entered a "zero" value for acceleration. Above there are two calculations. The first is for a vehicle speed of 50 kph, and after taking into account drive-train inefficiency, this web-calculator produced a figure of 132 KW. The second is for a vehicle speed of 68 kph, which of course is slightly different than a vehicle speed of 50 kph + 18 kph for headwind. Even still, this calculator produced a final figure of 198.4 KW. The first figure is less than our calculated 146.8 KW per hour using Iain's formulas, but the second figure is significantly more, about 50 KW more. On the other hand, our Froll and Fair figures using Iain's formulas are only 16 KW lower per hour than those produced by the first web-calculator.
So at the very beginning, all of this should suggest that any calculations of possible TerraLiner power requirements should be taken with a grain of salt. These two web-calculators are not up-front about the formulas they use, so who knows what might account for the discrepancy in their computations. But the mere fact that I inserted identical values in both, and got somewhat divergent results, seems to suggest that both contain hidden assumptions that are skewing results one way or the other. As the second calculator warns:
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
7. The TerraLiner power requirement for a given for distance
**************************************************
Now this figure is only for one hour, but the ascent will take longer than that. Think of it this way: in the equations above, did a variable for "distance" appear even once? 146.8 KW represents the amount of power required to keep the TerraLiner ascending this slope per hour in perpetuity. It's not an absolute total of power consumption, but rather, it's a scalar value. Multiplying this value by time, we then get the total absolute amount of power needed.
The journey is a distance of 128.6 km, so at 50 kph it would take 2.57 hours. Therefore the total amount of power for the duration needed would be 2.57 x 146.8 KW = 377.28 KW.
In short, even in this minimal scenario, if only the 120 KW Jenoptik had been running it would have proven insufficient, because 120 KW x 2.57 = 308.4 KW:
For more information about the Jenoptik generator, see post #673 at http://www.expeditionportal.com/for...igid-Torsion-Free-Frame?p=1670215#post1670215 .
If we then posit draining down a 100 KW battery pack over the course of 2 ½ hours, we’d have 408.4 KW available: 308.4 KW from the Jenoptik + 100 KW from the battery. So at the summit, we might still have about 30 KW left in the battery. This may seem like a wonderful result, but this is is the slowest and least-challenging scenario. It may seem to demonstrate that if we had just one Jenoptik generator + a 100 KW battery pack functioning as a “fail safe”, long inclines could indeed still be climbed, albeit at the slow speed of 50 kph. And as long as they are relatively "moderate" long inclines, with slope-gradients of just 1.4 %.....:sombrero:...
But the power result produced by the second web-calculator -- 198.4 KW per hour -- should give us pause for thought. Multiplied by 2.57 hours, we would get a total power requirement of 509.9 KW, which is about 100 KW in excess of the power available from just one Jenoptik generator + a 100 KW battery pack. So it seems fairly clear right at the beginning that just one Jenoptik generator + a 100 KW battery bank simply won't be enough.
**************************************************
8. Sea level to Monarch Pass, assuming a 3 % ascent, from zero to 3,858 m
**************************************************
What if we change the parameters to an imagine a more hypothetical scenario, ascending from sea level to Monarch Pass along the same distance, 128.6 km, but ending up slightly higher, at 3,858 m? The gradient would then be 3 %. But still ascending at 50 kph, with a moderate headwind of 18 kph, and so a total speed relative to the air of 19 m/s.
In this scenario Froll and Fair stay the same, but Fslope increases from 4,394.9 kg m/s[SUP]2 [/SUP]to 9,417.6 kg m/s[SUP]2[/SUP], and Ftotal increases to 3139.2 kg m/s[SUP]2[/SUP] + 9,417.6 kg m/s[SUP]2 [/SUP]+ 1979.18 m/s[SUP]2[/SUP] = 14,535.98 kg m/s[SUP]2[/SUP]. Multiplying this figure by the vehicle’s velocity of 13.9 m/s (which does not have to include windspeed!), we get 202,050 kg m[SUP]2[/SUP]/s[SUP]3[/SUP], or 202 KW per hour. Quite an increase. We still have to divide by 0.90 to account for a 10 % loss of efficiency from the Hub-motor gearing, so we get 224.4 KW.
But that’s only for one hour, and we have to multiply by 2.57 hours, yielding a final figure of 576.82 KW for the duration. This is now about 168 KW short of the 408.4 KW that we just calculated for a single Jenoptik generator working in concert with a 100 KW battery pack. Even doubling the battery-pack to 200 KW, the TerraLiner would still be 68 KW short. Whereas if the generator had produced about 70 KW more power per hour (i.e. if it were rated for 190 KW, instead of 120 KW), then the battery-pack could have stayed the same size, just 100 KW.
**************************************************
9. Double-Checking our Figures against On-Line Web Calculators:
**************************************************
Now let's double-check with our on-line web-calculators. The first does not calculate Fslope, and the figures it provides for Froll and Fair will remain the same. If we use this calculator's combined power figure for Fslope + Fair, which as we saw was about 16 KW more than the figure we obtained using Iain's equations, then we merely have to add 16 KW per hour, or 41.12 KW, to arrive at a final power figure for the entire slope of 617.94 KW. Call it 618 KW.
In the case of the second web-calcuator, the final power figure is quite different from our result -- again, see http://buggies.builtforfun.co.uk/Calculator/index.html . After deducting for hub-gearbox inefficiency, the second web-calculator gives an hourly figure of 304.5 KW, or roughy 80 KW more than what we calculated using Iain's equations:
Multiplying 304.5 KW by 2.57 hours, we get a final power figure of 782.57 KW for the whole 128.6 miles. This is now 374.17 KW short of the 408.4 KW we just calculated as the power supplied by a single Jenoptik generator used in concert with a 100 KW battery pack. Even doubling the battery-pack to 200 KW, the TerraLiner would still be 274.17 KW short. So if we take this second web-calculator seriously, then even with a 200 KW battery pack, we would still need the generator to produce about 110 KW more power per hour, i.e. we'd need the genertoar to be rated for 230 KW, instead of 120 KW.
Now my own view is that driving up a 3 % slope for about 2 ½ hours is the most extreme scenario that the TerraLIner will actually encounter in the real world. And not a 5 % slope for the same distance. I could be wrong about this. But I have a feeling that even the most challenging mountain passes will still only have sections that rise at a 5 % gradient. Sure, there are even 7 % gradients in certain sections of the Route 50 near the Monarch pass, and there is a short, 7-mile stretch of the Eisenhower pass that has a 7 % gradient. But mountain ascents will not rise on average 5 %, to gain more than 6,430 m in altitude over the course of just 128.6 km. I defy any thread participant to find a road that ascends from sea level (or close enough) to 6,430 m. Just in case anyone cares to look, the altitude alone is impossible, because the highest motorable road in the world tops out at 5,359 m – see https://en.wikipedia.org/wiki/Khardung_La.
I could be wrong about this, but I really do think that a 3 % slope (on average) for 2 ½ hours at 50 kph is about the limit. If anyone reading this finds a road ascent more challenging than that, please post!! It would be especially valuable if someone might post an example of a 5 % gradient that runs longer than 50 km, or a 7 % gradient that runs longer than 20 km.
However, such reflections do suggest at least this much. The TerraLiner’s battery pack probably should be more like 200 KW instead of 100 KW, and its primary generator probably should produce more like 150 – 180 KW (at a minimum), instead of 120 KW. In fact, if we take the power figure produced by the second web-calculator seriously, 782.57 KW, then the TerraLiner's primary generator should be rated for roughly 240 - 260 KW of output. That way, even if the supplementary second generator was broken, the primary generator would still have the “fail safe” ability to climb a 3 % gradient for 2 ½ hours at 50 kph with moderate headwind. Without this "fail safe" built in, if the second generator did not work, the TerraLiner might find itself stuck.
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
7. The TerraLiner power requirement for a given for distance
**************************************************
Now this figure is only for one hour, but the ascent will take longer than that. Think of it this way: in the equations above, did a variable for "distance" appear even once? 146.8 KW represents the amount of power required to keep the TerraLiner ascending this slope per hour in perpetuity. It's not an absolute total of power consumption, but rather, it's a scalar value. Multiplying this value by time, we then get the total absolute amount of power needed.
The journey is a distance of 128.6 km, so at 50 kph it would take 2.57 hours. Therefore the total amount of power for the duration needed would be 2.57 x 146.8 KW = 377.28 KW.
In short, even in this minimal scenario, if only the 120 KW Jenoptik had been running it would have proven insufficient, because 120 KW x 2.57 = 308.4 KW:
For more information about the Jenoptik generator, see post #673 at http://www.expeditionportal.com/for...igid-Torsion-Free-Frame?p=1670215#post1670215 .
If we then posit draining down a 100 KW battery pack over the course of 2 ½ hours, we’d have 408.4 KW available: 308.4 KW from the Jenoptik + 100 KW from the battery. So at the summit, we might still have about 30 KW left in the battery. This may seem like a wonderful result, but this is is the slowest and least-challenging scenario. It may seem to demonstrate that if we had just one Jenoptik generator + a 100 KW battery pack functioning as a “fail safe”, long inclines could indeed still be climbed, albeit at the slow speed of 50 kph. And as long as they are relatively "moderate" long inclines, with slope-gradients of just 1.4 %.....:sombrero:...
But the power result produced by the second web-calculator -- 198.4 KW per hour -- should give us pause for thought. Multiplied by 2.57 hours, we would get a total power requirement of 509.9 KW, which is about 100 KW in excess of the power available from just one Jenoptik generator + a 100 KW battery pack. So it seems fairly clear right at the beginning that just one Jenoptik generator + a 100 KW battery bank simply won't be enough.
**************************************************
8. Sea level to Monarch Pass, assuming a 3 % ascent, from zero to 3,858 m
**************************************************
What if we change the parameters to an imagine a more hypothetical scenario, ascending from sea level to Monarch Pass along the same distance, 128.6 km, but ending up slightly higher, at 3,858 m? The gradient would then be 3 %. But still ascending at 50 kph, with a moderate headwind of 18 kph, and so a total speed relative to the air of 19 m/s.
In this scenario Froll and Fair stay the same, but Fslope increases from 4,394.9 kg m/s[SUP]2 [/SUP]to 9,417.6 kg m/s[SUP]2[/SUP], and Ftotal increases to 3139.2 kg m/s[SUP]2[/SUP] + 9,417.6 kg m/s[SUP]2 [/SUP]+ 1979.18 m/s[SUP]2[/SUP] = 14,535.98 kg m/s[SUP]2[/SUP]. Multiplying this figure by the vehicle’s velocity of 13.9 m/s (which does not have to include windspeed!), we get 202,050 kg m[SUP]2[/SUP]/s[SUP]3[/SUP], or 202 KW per hour. Quite an increase. We still have to divide by 0.90 to account for a 10 % loss of efficiency from the Hub-motor gearing, so we get 224.4 KW.
But that’s only for one hour, and we have to multiply by 2.57 hours, yielding a final figure of 576.82 KW for the duration. This is now about 168 KW short of the 408.4 KW that we just calculated for a single Jenoptik generator working in concert with a 100 KW battery pack. Even doubling the battery-pack to 200 KW, the TerraLiner would still be 68 KW short. Whereas if the generator had produced about 70 KW more power per hour (i.e. if it were rated for 190 KW, instead of 120 KW), then the battery-pack could have stayed the same size, just 100 KW.
**************************************************
9. Double-Checking our Figures against On-Line Web Calculators:
**************************************************
Now let's double-check with our on-line web-calculators. The first does not calculate Fslope, and the figures it provides for Froll and Fair will remain the same. If we use this calculator's combined power figure for Fslope + Fair, which as we saw was about 16 KW more than the figure we obtained using Iain's equations, then we merely have to add 16 KW per hour, or 41.12 KW, to arrive at a final power figure for the entire slope of 617.94 KW. Call it 618 KW.
In the case of the second web-calcuator, the final power figure is quite different from our result -- again, see http://buggies.builtforfun.co.uk/Calculator/index.html . After deducting for hub-gearbox inefficiency, the second web-calculator gives an hourly figure of 304.5 KW, or roughy 80 KW more than what we calculated using Iain's equations:
Multiplying 304.5 KW by 2.57 hours, we get a final power figure of 782.57 KW for the whole 128.6 miles. This is now 374.17 KW short of the 408.4 KW we just calculated as the power supplied by a single Jenoptik generator used in concert with a 100 KW battery pack. Even doubling the battery-pack to 200 KW, the TerraLiner would still be 274.17 KW short. So if we take this second web-calculator seriously, then even with a 200 KW battery pack, we would still need the generator to produce about 110 KW more power per hour, i.e. we'd need the genertoar to be rated for 230 KW, instead of 120 KW.
Now my own view is that driving up a 3 % slope for about 2 ½ hours is the most extreme scenario that the TerraLIner will actually encounter in the real world. And not a 5 % slope for the same distance. I could be wrong about this. But I have a feeling that even the most challenging mountain passes will still only have sections that rise at a 5 % gradient. Sure, there are even 7 % gradients in certain sections of the Route 50 near the Monarch pass, and there is a short, 7-mile stretch of the Eisenhower pass that has a 7 % gradient. But mountain ascents will not rise on average 5 %, to gain more than 6,430 m in altitude over the course of just 128.6 km. I defy any thread participant to find a road that ascends from sea level (or close enough) to 6,430 m. Just in case anyone cares to look, the altitude alone is impossible, because the highest motorable road in the world tops out at 5,359 m – see https://en.wikipedia.org/wiki/Khardung_La.
I could be wrong about this, but I really do think that a 3 % slope (on average) for 2 ½ hours at 50 kph is about the limit. If anyone reading this finds a road ascent more challenging than that, please post!! It would be especially valuable if someone might post an example of a 5 % gradient that runs longer than 50 km, or a 7 % gradient that runs longer than 20 km.
However, such reflections do suggest at least this much. The TerraLiner’s battery pack probably should be more like 200 KW instead of 100 KW, and its primary generator probably should produce more like 150 – 180 KW (at a minimum), instead of 120 KW. In fact, if we take the power figure produced by the second web-calculator seriously, 782.57 KW, then the TerraLiner's primary generator should be rated for roughly 240 - 260 KW of output. That way, even if the supplementary second generator was broken, the primary generator would still have the “fail safe” ability to climb a 3 % gradient for 2 ½ hours at 50 kph with moderate headwind. Without this "fail safe" built in, if the second generator did not work, the TerraLiner might find itself stuck.
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
10. A 200 KW battery pack?
**************************************************
A 200 KW battery pack would have the added virtue that it could provide the TerraLiner when glamping with up to 20 days of continuous, generator-free power, if the power consumption of the camper box when stationary was 10 KW per day. And a 200 KW battery pack could still provide 10 days of power if consumption were 20 KW per day. So when glamping in an equatorial country with low wind-speed and poor solar irradiation, because it's raining all the time, at the most the TerraLiner would only have to run its generator just once every 10 days to recharge the batteries -- if in fact power consumption was just 20 KW per day. However, for reasons I will explain further along, I suspect that it would be considerably more than that.
If the TerraLiner were to use a state-of-the-art battery pack of the kind developed by Proterra, where 8 of its extended-range “packs” combined can now yield 257 KWH, and 6 of its extended-range packs would presumably yield 192.75 KW, then those 6 packs would weigh 770 lbs each, or roughly 350 kg, for a total of 2100 kg – see http://www.proterra.com/wp-content/uploads/2015/05/Tearsheets_CatalystPlatform.pdf and http://www.proterra.com/wp-content/uploads/2015/05/Tearsheets_ExtendedRange.pdf , and see post #1918 for at http://www.expeditionportal.com/for...igid-Torsion-Free-Frame?p=1959999#post1959999 , for a full discussion of Proterra:
Although Proterra's latest design (2015) does not quite reach 1 ton per 100 KW, for the rest of the thread let's simply assume that the TerraLiner's batteries will probably weigh about that much. If the TerraLiner were fabricated circa 2020, perhaps the batteries installed might yield 20 - 40 % more energy, but in all likelihood not more than that.
Now a two-ton battery pack is not insignificant. If the power-consumption figure that we arrived at using Iain's equations were more nearly right (576.82 KW for the 128.6 km of the slope), then if we merely increased the size of the primary generator from 120 KW to 190 KW, we could save 1 ton of weight, or 1,000 kg. The battery pack could remain 100 KW, instead of increasing to 200 KW. I strongly suspect that if we moved from a 120 KW Jenoptik that weighs 350 kg, to another generator that produces 190 KW, the weight would at the very most double, adding at most only another 350 kg.
On the other hand, suppose that the web-calcuator's figure of of 782.565 KW for the whole 128.6 miles is right. Adding a third Jenoptik generator would add just another 350 kg, but would dramatically increase the power available to climb a slope from 120 KW to 240 KW per hour. Over the course of 2.57 hours we'd have 616.8 KW available from the two Jenoptik generators, + 100 KW from the battery pack, or 716.8 KW in total. In this second scenario we would still be about 70 KW short, so the battery bank would still need to be 200 KW after all. But at least we would only be adding 100 KW of batteries, and not 400 KW of batteries. In other words, we'd only be adding 1 ton of weight, instead of an additional 4 tons!
Such calculations alone should suggest why adding more batteries is never a “good deal” from the point of view of the weight-to-power ratio. In the first 576.82 KW power scenario, if the degree of fail-safe operation that I've just sketched were desired, then simply increasing the size of the generator to 190 KW would be much more optimal from a weight point of view, because at most we'd be adding only 350 kg of weight for a larger generator, instead of 1000 kg for batteries. And in the second scenario, where total power consumption for the duration is 782.565 KW, we'd only add 350 kg for a third Jenoptik generator + 1000 kg to increase the size of the battery pack to 200 KW, instead of adding another 4000 kg for batteries alone.
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
10. A 200 KW battery pack?
**************************************************
A 200 KW battery pack would have the added virtue that it could provide the TerraLiner when glamping with up to 20 days of continuous, generator-free power, if the power consumption of the camper box when stationary was 10 KW per day. And a 200 KW battery pack could still provide 10 days of power if consumption were 20 KW per day. So when glamping in an equatorial country with low wind-speed and poor solar irradiation, because it's raining all the time, at the most the TerraLiner would only have to run its generator just once every 10 days to recharge the batteries -- if in fact power consumption was just 20 KW per day. However, for reasons I will explain further along, I suspect that it would be considerably more than that.
If the TerraLiner were to use a state-of-the-art battery pack of the kind developed by Proterra, where 8 of its extended-range “packs” combined can now yield 257 KWH, and 6 of its extended-range packs would presumably yield 192.75 KW, then those 6 packs would weigh 770 lbs each, or roughly 350 kg, for a total of 2100 kg – see http://www.proterra.com/wp-content/uploads/2015/05/Tearsheets_CatalystPlatform.pdf and http://www.proterra.com/wp-content/uploads/2015/05/Tearsheets_ExtendedRange.pdf , and see post #1918 for at http://www.expeditionportal.com/for...igid-Torsion-Free-Frame?p=1959999#post1959999 , for a full discussion of Proterra:
Although Proterra's latest design (2015) does not quite reach 1 ton per 100 KW, for the rest of the thread let's simply assume that the TerraLiner's batteries will probably weigh about that much. If the TerraLiner were fabricated circa 2020, perhaps the batteries installed might yield 20 - 40 % more energy, but in all likelihood not more than that.
Now a two-ton battery pack is not insignificant. If the power-consumption figure that we arrived at using Iain's equations were more nearly right (576.82 KW for the 128.6 km of the slope), then if we merely increased the size of the primary generator from 120 KW to 190 KW, we could save 1 ton of weight, or 1,000 kg. The battery pack could remain 100 KW, instead of increasing to 200 KW. I strongly suspect that if we moved from a 120 KW Jenoptik that weighs 350 kg, to another generator that produces 190 KW, the weight would at the very most double, adding at most only another 350 kg.
On the other hand, suppose that the web-calcuator's figure of of 782.565 KW for the whole 128.6 miles is right. Adding a third Jenoptik generator would add just another 350 kg, but would dramatically increase the power available to climb a slope from 120 KW to 240 KW per hour. Over the course of 2.57 hours we'd have 616.8 KW available from the two Jenoptik generators, + 100 KW from the battery pack, or 716.8 KW in total. In this second scenario we would still be about 70 KW short, so the battery bank would still need to be 200 KW after all. But at least we would only be adding 100 KW of batteries, and not 400 KW of batteries. In other words, we'd only be adding 1 ton of weight, instead of an additional 4 tons!
Such calculations alone should suggest why adding more batteries is never a “good deal” from the point of view of the weight-to-power ratio. In the first 576.82 KW power scenario, if the degree of fail-safe operation that I've just sketched were desired, then simply increasing the size of the generator to 190 KW would be much more optimal from a weight point of view, because at most we'd be adding only 350 kg of weight for a larger generator, instead of 1000 kg for batteries. And in the second scenario, where total power consumption for the duration is 782.565 KW, we'd only add 350 kg for a third Jenoptik generator + 1000 kg to increase the size of the battery pack to 200 KW, instead of adding another 4000 kg for batteries alone.
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
...
CONTINUED FROM PREVIOUS POST
**************************************************
11. The Problem with Batteries
**************************************************
Although I am very clearly a dreamer, otherwise I would not have developed this thread, at the same time I really enjoy "tracking" technological reality. Design is more fun that way, because things get too wide-open and "science fiction" (to borrow campo's apt description!!) if one helps oneself to whatever purely hypothetical technology one likes. The dance here on Iain's "bleeding edge" is clearly a challenging one, and different participants will have different ideas about where and how we should dance with regard to a specific engineering issue. But on my own view, anyone who reads enough automotive and engineering literature about batteries, hybrid vehicles, and all-electric cars, must come to one and only one conclusion: battery development has been slow, and will continue to be slow. And batteries may never match the power density of fossil fuels.
Now granted, where science and technology are concerned, it's probably a good idea to never say never. Just recently I myself posted a link to an article in the most recent issue of the Cambridge alum magazine, an article that describes research on Lithium-Air batteries, batteries that may in fact reach the holy grail of power-density parity with fossil fuels -- see https://www.alumni.cam.ac.uk/magazine , http://www.cam.ac.uk/research/news/new-design-points-a-path-to-the-ultimate-battery , http://www.bbc.com/news/science-environment-34670919 , and http://www.gizmag.com/lithium-air-battery-university-cambridge/40411/ . But Lith-Air batteries are still at least a decade away from being commercially available, and most of the other battery technologies that might take us beyond Lith-Ion all have problems:
The barriers to increased battery performance are very formidable:
See http://spectrum.ieee.org/semiconduc...capacitor-will-supercharge-mobile-electronics . Super-thin supercapacitors may provide a power breakthrough for devices that need just a spurt of power, but they won't be a replacement any time soon for deep-cylce batteries, because supercapacitors have a comparatively low energy storage ability.
The following article in particular makes for very sobering reading, and should be appreciated in full -- see http://physics.ucsd.edu/do-the-math/2012/08/battery-performance-deficit-disorder/ :
Also see http://physics.ucsd.edu/do-the-math/2012/08/battery-performance-deficit-disorder/ and http://www.aps.org/publications/apsnews/201207/electriccars.cfm .
The following chart, if read properly, should say it all:
But because some thread participants may not properly understand a chart whose axes have scales that are logarithmic (see https://en.wikipedia.org/wiki/Logarithmic_scale ), I will quote once more from the same article above, to drive home the point with full force:
Yes, that's right: 400 times. ICE engines and their fuel tanks do not have power-weight ratios that are merely twice those of current batteries, and not merely 10 times. Rather, ICE engines and their fuel tanks are 400 times more energy-dense. That should be a a sobering thought that cuts through a great deal of nonsense.
Yes, I still think it makes sense to develop a "fully hybrid" TerraLiner, one that has a fairly big battery bank (200 KW), and enormous electric hub motors, the latter mainly to serve as retarders when braking. The resulting vehicle may indeed prove to be a bit more fuel efficient (say 10 - 20 %) because of regenerative braking, i.e. more fuel efficient than a premium Class-A motorhome of equivalent size powered by a 600 or 700 HP ICE.
But the main reason for developing such a hybrid is not in order to fantasize about reducing the size of the ICE generators to nearly nothing, replacing them with stupendously and stupidly heavy battery packs instead. At this point in history that's a fool's fantasy, and only someone who is not reading serious hybrid engineering and automotive literature would ever propose such a fantasy for a long-haul bus, truck, or motorhome circa 2020. Rather, the reason to develop a fully hybrid TerraLiner, is because -- as Haf-E has repeated throughout the thread -- with a serial hybrid drivetrain we get:
(1) Fail-Safe design, with redundant systems, and no single point of failure
(2) Easily interchangeable components
(3) The design flexibility that full serial hybridity allows, providing an "Open Generator Architecture"
(4) The ability to distribute drive-train components more evenly, for better overall vehicle balance
(5) The ability to place the generators in locations other than forward and aft, opening up the front and back of the TerraLiner to further design possibilities
In addition, if the TerraLiner were equipped with a 200 KW battery bank, it would then have the ability to run all camper-box systems at full blast for 10 days, off the battery bank alone, without any input whatsoever from solar, wind, or the generators. This too strikes me as tremendously attractive. Which might incline us towards a 200 KW battery pack, despite the added 1000 kg of weight. But it would be this "glamping-in-silence" consideration that tips the scales in favor of a bigger, 200 KW battery pack, and not the slope-climbing requirements of the TerraLiner.
These are the reasons why a fully hybrid TerraLiner interests me. Others may have different motivations, and it has become clear that some thread participants are "all-electric zealots" who dream of eliminating ICE engines completely. So for the record, I am not one of them, and this is not the reason why a fully hybrid TerraLiner interests me. It's just too clear to me that batteries are a very bad deal from the point of view of the weight-to-power ratio, and that they will remain so for a very long time to come, for at least another 10 years, and possibly 15 - 20 years.
This was the essence of the point that Iain was making when he first provided the thread with his power calculations. Namely, that current deep-cycle batteries simply do not have anything like the same energy density as diesel fuel combined with an ICE.
Those who "believe in batteries" -- those who are battery-fundamentalists unsatisfied by anything less than the holy grail of the "all-electric vehicle" -- are generally immune to such basic facts. The automotive industry is densely populated with such "true believers" or "battery purists", and in some of his interviews Ian Wright talks talks eloquently about the obstacle that these true-believers pose. If they can't have the perfect all-battery solution, then they want no solution, and they want to stick with all-ICE. Whereas it will be precisely hybrid transitional vehicles that will get us from ICE to pure electric, with sales of hybrids providing the income stream to justify and support further battery research & development. Without that income stream, the "all-electric long-haul bus" or the "all-electric long-haul truck" will forever remain a pipe dream.
So Iain, your thoughts along these lines are very well-taken, and most welcome as a corrective antidote. As I have already stated a number of times, your "devil's advocacy" in this thread has been exemplary, because it has been driven by facts and arguments. But with that said, I am still interested in thinking through and designing a fully hybrid TerraLiner, for the reasons just given.....:sombrero:
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
11. The Problem with Batteries
**************************************************
Although I am very clearly a dreamer, otherwise I would not have developed this thread, at the same time I really enjoy "tracking" technological reality. Design is more fun that way, because things get too wide-open and "science fiction" (to borrow campo's apt description!!) if one helps oneself to whatever purely hypothetical technology one likes. The dance here on Iain's "bleeding edge" is clearly a challenging one, and different participants will have different ideas about where and how we should dance with regard to a specific engineering issue. But on my own view, anyone who reads enough automotive and engineering literature about batteries, hybrid vehicles, and all-electric cars, must come to one and only one conclusion: battery development has been slow, and will continue to be slow. And batteries may never match the power density of fossil fuels.
Now granted, where science and technology are concerned, it's probably a good idea to never say never. Just recently I myself posted a link to an article in the most recent issue of the Cambridge alum magazine, an article that describes research on Lithium-Air batteries, batteries that may in fact reach the holy grail of power-density parity with fossil fuels -- see https://www.alumni.cam.ac.uk/magazine , http://www.cam.ac.uk/research/news/new-design-points-a-path-to-the-ultimate-battery , http://www.bbc.com/news/science-environment-34670919 , and http://www.gizmag.com/lithium-air-battery-university-cambridge/40411/ . But Lith-Air batteries are still at least a decade away from being commercially available, and most of the other battery technologies that might take us beyond Lith-Ion all have problems:
The barriers to increased battery performance are very formidable:
See http://spectrum.ieee.org/semiconduc...capacitor-will-supercharge-mobile-electronics . Super-thin supercapacitors may provide a power breakthrough for devices that need just a spurt of power, but they won't be a replacement any time soon for deep-cylce batteries, because supercapacitors have a comparatively low energy storage ability.
The following article in particular makes for very sobering reading, and should be appreciated in full -- see http://physics.ucsd.edu/do-the-math/2012/08/battery-performance-deficit-disorder/ :
Also see http://physics.ucsd.edu/do-the-math/2012/08/battery-performance-deficit-disorder/ and http://www.aps.org/publications/apsnews/201207/electriccars.cfm .
The following chart, if read properly, should say it all:
But because some thread participants may not properly understand a chart whose axes have scales that are logarithmic (see https://en.wikipedia.org/wiki/Logarithmic_scale ), I will quote once more from the same article above, to drive home the point with full force:
Yes, that's right: 400 times. ICE engines and their fuel tanks do not have power-weight ratios that are merely twice those of current batteries, and not merely 10 times. Rather, ICE engines and their fuel tanks are 400 times more energy-dense. That should be a a sobering thought that cuts through a great deal of nonsense.
Yes, I still think it makes sense to develop a "fully hybrid" TerraLiner, one that has a fairly big battery bank (200 KW), and enormous electric hub motors, the latter mainly to serve as retarders when braking. The resulting vehicle may indeed prove to be a bit more fuel efficient (say 10 - 20 %) because of regenerative braking, i.e. more fuel efficient than a premium Class-A motorhome of equivalent size powered by a 600 or 700 HP ICE.
But the main reason for developing such a hybrid is not in order to fantasize about reducing the size of the ICE generators to nearly nothing, replacing them with stupendously and stupidly heavy battery packs instead. At this point in history that's a fool's fantasy, and only someone who is not reading serious hybrid engineering and automotive literature would ever propose such a fantasy for a long-haul bus, truck, or motorhome circa 2020. Rather, the reason to develop a fully hybrid TerraLiner, is because -- as Haf-E has repeated throughout the thread -- with a serial hybrid drivetrain we get:
(1) Fail-Safe design, with redundant systems, and no single point of failure
(2) Easily interchangeable components
(3) The design flexibility that full serial hybridity allows, providing an "Open Generator Architecture"
(4) The ability to distribute drive-train components more evenly, for better overall vehicle balance
(5) The ability to place the generators in locations other than forward and aft, opening up the front and back of the TerraLiner to further design possibilities
In addition, if the TerraLiner were equipped with a 200 KW battery bank, it would then have the ability to run all camper-box systems at full blast for 10 days, off the battery bank alone, without any input whatsoever from solar, wind, or the generators. This too strikes me as tremendously attractive. Which might incline us towards a 200 KW battery pack, despite the added 1000 kg of weight. But it would be this "glamping-in-silence" consideration that tips the scales in favor of a bigger, 200 KW battery pack, and not the slope-climbing requirements of the TerraLiner.
These are the reasons why a fully hybrid TerraLiner interests me. Others may have different motivations, and it has become clear that some thread participants are "all-electric zealots" who dream of eliminating ICE engines completely. So for the record, I am not one of them, and this is not the reason why a fully hybrid TerraLiner interests me. It's just too clear to me that batteries are a very bad deal from the point of view of the weight-to-power ratio, and that they will remain so for a very long time to come, for at least another 10 years, and possibly 15 - 20 years.
This was the essence of the point that Iain was making when he first provided the thread with his power calculations. Namely, that current deep-cycle batteries simply do not have anything like the same energy density as diesel fuel combined with an ICE.
Those who "believe in batteries" -- those who are battery-fundamentalists unsatisfied by anything less than the holy grail of the "all-electric vehicle" -- are generally immune to such basic facts. The automotive industry is densely populated with such "true believers" or "battery purists", and in some of his interviews Ian Wright talks talks eloquently about the obstacle that these true-believers pose. If they can't have the perfect all-battery solution, then they want no solution, and they want to stick with all-ICE. Whereas it will be precisely hybrid transitional vehicles that will get us from ICE to pure electric, with sales of hybrids providing the income stream to justify and support further battery research & development. Without that income stream, the "all-electric long-haul bus" or the "all-electric long-haul truck" will forever remain a pipe dream.
So Iain, your thoughts along these lines are very well-taken, and most welcome as a corrective antidote. As I have already stated a number of times, your "devil's advocacy" in this thread has been exemplary, because it has been driven by facts and arguments. But with that said, I am still interested in thinking through and designing a fully hybrid TerraLiner, for the reasons just given.....:sombrero:
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
12. Cañon City to Monarch Pass, at 90 kph without headwind
**************************************************
So far then:
As Iain has suggested a few times, increasing velocity will significantly increase the per-hour power requirement, because air-resistance is a cubic function, multiplying velocity by the power of 3. However, the actual outcome for power consumption for a given distance is more complicated than that, because once we specify a given distance in terms of time, in effect we re-introduce "v" (for velocity), but this time dividing by v. So v[SUP]3 [/SUP]actually becomes v[SUP]2[/SUP]. This insight is nicely summarized by the following statement -- see http://www.truck-drivers-money-saving-tips.com/air-resistance.html :
This is a somewhat complex idea, so before explaining it further, let's see how some additional power calculations work out.
Calculating for a speed of 90 kph without headwind (25 m/s), the distance is still Cañon City to Monarch Pass, or 128.6 km, the slope is still 1.4 %, and so it's the third equation for Fair that will change, because the air-velocity becomes 90 kph, or 25 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (25 m/s)[SUP] 2[/SUP])/2 = 6853.13 m/s[SUP]2 [/SUP]divided by 2 = 3426.56 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 3426.56 m/s[SUP]2[/SUP]= 10,960.66 kg m/s[SUP]2 [/SUP].
Multiplying the second figure for FTotal by the TerraLiner's velocity of 25 m/s, we get 274,016.5 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 274KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 304.4 KW.
This may seem like an even more dramatic increase for the power requirement than merely raising the slope to 3 %, which one might recall was 224.4 KW at this point. And here one might be tempted to say that working against air pressure is much more challenging than working against gravity. But that would be premature, because our calculation is not quite finished yet.
The TerraLiner is now traveling at 90 kph instead of 50 kph, so the travel time will be shorter, 1.43 hours, or about 1 hour and 26 minutes. Multiplying, we get 304.4 KW x 1.43 = 435.4 KW, which is considerably less than the 576.82 KW that we calculated to climb a slope of 3 % at 50 kph with an 18 kph headwind.
On the other hand, this figure of 435.4 KW is 60 KW more than the power figure --- 377.28 KW -- for climbing a slope of 1.4 % at 50 kph with an 18 kph headwind (i.e. 68 kph); see Section 7 above in post #2107 at http://www.expeditionportal.com/for...w-6x6-Hybrid-Drivetrain?p=1973664#post1973664 . Which is perhaps what we should expect: why would adding 22 kph change things that much?
But again, before we jump to conclusions, let's input the same amounts into our web-calculators, to see what we get.
Using the first web-calculator, all we need do is consult the table that it produced the first time around, now looking for a value closest to 90 kph. As luck would have it, 89 kph is listed as a value, and the table states that the Wattage required for Froll + Fair is 158,837.58 W, or 158.8 KW:
But in order to be precise, let's pro-rate this upwards, adding the difference between 190,214.72 - 158,837.58 W, divided by 8, or 31,377.14 / 8 = 3,922.14 W. 158,837.58 W + 3,922.14 W = 162,759.72 W, or 162.8 KW.
All we need to do now is add the power requirement for Fslope as calculated using Iain's equation. For a 1.4 % grade this was 4,394.9 kg m/s[SUP]2[/SUP]. Multiplying by 25 m/s (90 kph), we get 109,9872.5 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 109.99 KW. Dividing by 0.9 for hub-gear inefficiency, we get 122 KW per hour. We then add this to the web-calculator's figure for Froll + Fslope (this figure already includes a discount for hub-gear inefficiency), and we arrive at the per-hour consumption figure of 162.8 KW + 122 KW = 284.8 KW. Which, happily enough, is numeric value rather similar to the figure we arrived at using Iain's equations, namely 304.4 KW. Only about 20 KW off. So far so good.
In the case of the second web-calculator, we seem to be even more "on the right track". The final value it gives once hub-gear inefficiency is deducted is 303.5 KW, almost identical to the value we obtained using Iain's equations, 304.4 KW:
Multiplying this figure by 1.43 hours, we get 434 KW for the duration.
**************************************************
13. Cañon City to Monarch Pass, at 90 kph with 18 kph headwind
**************************************************
Now let's calculate what happens when we add on another 18 kph for headwind to 90 kph, for a total air-velocity of 30 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (30 m/s)[SUP] 2[/SUP])/2 = 9868.5 m/s[SUP]2 [/SUP]divided by 2 = 4934.25 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 4,934.25 m/s[SUP]2[/SUP]= 12,468.35 kg m/s[SUP]2 [/SUP].
Multiplying this figure for FTotal by the TerraLiner's velocity of 25 m/s (the velocity without headwind), we get 311,708.75 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 311.7 KW per hour. We divide by 0.90 for hub-gear inefficiency and get 346.3 KW. Again travel time is 1.43 hours, or about 1 hour and 26 minutes, so our final figure is 346.3 KW x 1.43 = 495.3 KW.
**************************************************
IMPORTANT NOTE: throughout these calculations, in my final multiplication to get a power figure in Watts, I will be using the TerraLiner's velocity relative to the ground, and not its air-speed velocity. If I were to use the latter velocity, then I would be multiplying Froll and Fslope by the air-speed velocity, which seems just plain wrong. Perhaps a more accurate calculation would multiply Froll and Fslope by the TerraLiner's velocity relative to the gourd, and then a second calculation would multiple Fair by the airspeed velocity? That way one might get a more accurate representation of air-resistance as a cubic function, as v[SUP]3 [/SUP]. But Iain suggested simply multiplying the final sum of FTotal by the TerraLiner's velocity, so that's what I will be doing......
**************************************************
Now notice that when using Iain's equations, there is a 120 KW difference between the total or "absolute" amount of power required to climb this slope up to Monarch Pass at 50 kph with an 18 kph headwind (377.28 KW), versus the power required to climb the same slope at 90 kph with an 18 kph headwind (495.3 KW). Also notice the slightly non-linear progression. As we increased the airspeed from 68 kph to 90 kph, or 22 kph, the power consumption increased about 60 W. Now we are increasing the TerraLiner's airspeed just another 18 kph, and the power consumption jumps another 60 W. But the difference is not "dramatically" non-linear.
Again, before we jump to conclusions, let's use our web-calculators to confirm that we are roughly on the right track.
In the case of the first web-calculator, consulting the table that it produces we now look for values that are closest to 108 kph (i.e. 90 kph + 18 kph). Turns out there are values for 105 kph and 113 kph, so "averaging", we get a power figure for 108 kph of 241,228.67 W, or 241.2 KW:
"Averaging" is not perfect, because the increase in the values for power on this table are non-linear. But for my present purposes averaging will suffice.
Fslope is still the same, so all we need to do is add 122 KW + 241.2 KW, and we arrive at the per-hour consumption figure of 363.2 KW. This is only a bit different -- about 17 KW different -- than the power figure that we arrived at using Iain's equations, i.e. 346.3 KW per hour. In the previous comparison, the figure arrived at using the web-calculator was 20 KW less; in this case, 17 KW more. The difference could probably be accounted for by the fact that at the end of Iain's equations I only multiplied by 25 m/s, and not by 30 m/s, for the reason given. Whereas this web-calculator no doubt multiples Froll + Fair by 30 m/s, because it has no way of distinguishing between the speed of the TerraLiner relative to the air, versus the speed of the TerraLiner relative to the ground. So far so good.
In the case of the second web-calculator, however, our calculation using Iain's equations seems to be quite a bit more "off":
There is a big difference between 346.3 KW per hour, versus 414.4 KW per hour. But I think it can be explained, along with a few other anomalies that are cropping up.
The absolute power requirement figures produced by the second web-calculator, i.e the power requirements for a given distance, seem at first to be positively confusing. When the second web-calculator computed the power required per hour for 50 kph with an 18 kph headwind, it arrived at a figure of 198.4 KW. Multiplying this by a total travel time of 2.57 hours, we arrived at total figure for the duration of 505.09 KW -- again, see Section 7 in post #2108 at http://www.expeditionportal.com/for...w-6x6-Hybrid-Drivetrain?p=1973665#post1973665 . Now that the travel time is just 1.43 hours, our final figure for the duration at 90 kph with 18 kph headwind is 414.4 KW x 1.43 = 592.45 KW. If anything, this is an even more moderate jump than the 120 KW we arrived at using Iain's equations, a difference of just 87 KW.
However in between, for 90 kph without headwind, we got 434 KW for the duration, which is a lot less than than the power requirement for 50 kph + 18 kph. This makes no sense, until we think about what headwind actually represents. Headwind is like adding speed, which requires more power to overcome air-resistance, but without any of the benefit for the total power consumption for a given distance that comes from higher speed, i.e. the ability to cover more distance in less time.
Add to this the fact that to represent "50 kph + 18 kph headwind", I simply entered 68 kph into the second web-calculator. So when making the final multiplication by v, it will have multiplied Ftotal not by the TerraLiner's ground-speed, but rather, it will have multiplied Ftotal by the TerraLiner's airspeed. These two factors combined should account for the reason why 434 KW required at 90 kph is so much less than 505.08 KW required at 50 kph + headwind. It's then interesting for me that when we run parallel calculations for 90 kph straight, with no headwind, Iain's equations and this second web-calculator produce nearly the same result.
Once again, let's collect a few more data points before jumping to conclusions.....
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
12. Cañon City to Monarch Pass, at 90 kph without headwind
**************************************************
So far then:
- in order to guarantee fail-safe capability, the TerraLiner's first, relatively low-powered primary generator should have a power output of 240 - 260 KW
- and it would also be good for "glamping in silence" for the TerraLiner's battery pack to be more like 200 KW instead of 100 KW, despite the extra 1000 kg of weight that this entails.
As Iain has suggested a few times, increasing velocity will significantly increase the per-hour power requirement, because air-resistance is a cubic function, multiplying velocity by the power of 3. However, the actual outcome for power consumption for a given distance is more complicated than that, because once we specify a given distance in terms of time, in effect we re-introduce "v" (for velocity), but this time dividing by v. So v[SUP]3 [/SUP]actually becomes v[SUP]2[/SUP]. This insight is nicely summarized by the following statement -- see http://www.truck-drivers-money-saving-tips.com/air-resistance.html :
This is a somewhat complex idea, so before explaining it further, let's see how some additional power calculations work out.
Calculating for a speed of 90 kph without headwind (25 m/s), the distance is still Cañon City to Monarch Pass, or 128.6 km, the slope is still 1.4 %, and so it's the third equation for Fair that will change, because the air-velocity becomes 90 kph, or 25 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (25 m/s)[SUP] 2[/SUP])/2 = 6853.13 m/s[SUP]2 [/SUP]divided by 2 = 3426.56 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 3426.56 m/s[SUP]2[/SUP]= 10,960.66 kg m/s[SUP]2 [/SUP].
Multiplying the second figure for FTotal by the TerraLiner's velocity of 25 m/s, we get 274,016.5 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 274KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 304.4 KW.
This may seem like an even more dramatic increase for the power requirement than merely raising the slope to 3 %, which one might recall was 224.4 KW at this point. And here one might be tempted to say that working against air pressure is much more challenging than working against gravity. But that would be premature, because our calculation is not quite finished yet.
The TerraLiner is now traveling at 90 kph instead of 50 kph, so the travel time will be shorter, 1.43 hours, or about 1 hour and 26 minutes. Multiplying, we get 304.4 KW x 1.43 = 435.4 KW, which is considerably less than the 576.82 KW that we calculated to climb a slope of 3 % at 50 kph with an 18 kph headwind.
On the other hand, this figure of 435.4 KW is 60 KW more than the power figure --- 377.28 KW -- for climbing a slope of 1.4 % at 50 kph with an 18 kph headwind (i.e. 68 kph); see Section 7 above in post #2107 at http://www.expeditionportal.com/for...w-6x6-Hybrid-Drivetrain?p=1973664#post1973664 . Which is perhaps what we should expect: why would adding 22 kph change things that much?
But again, before we jump to conclusions, let's input the same amounts into our web-calculators, to see what we get.
Using the first web-calculator, all we need do is consult the table that it produced the first time around, now looking for a value closest to 90 kph. As luck would have it, 89 kph is listed as a value, and the table states that the Wattage required for Froll + Fair is 158,837.58 W, or 158.8 KW:
But in order to be precise, let's pro-rate this upwards, adding the difference between 190,214.72 - 158,837.58 W, divided by 8, or 31,377.14 / 8 = 3,922.14 W. 158,837.58 W + 3,922.14 W = 162,759.72 W, or 162.8 KW.
All we need to do now is add the power requirement for Fslope as calculated using Iain's equation. For a 1.4 % grade this was 4,394.9 kg m/s[SUP]2[/SUP]. Multiplying by 25 m/s (90 kph), we get 109,9872.5 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 109.99 KW. Dividing by 0.9 for hub-gear inefficiency, we get 122 KW per hour. We then add this to the web-calculator's figure for Froll + Fslope (this figure already includes a discount for hub-gear inefficiency), and we arrive at the per-hour consumption figure of 162.8 KW + 122 KW = 284.8 KW. Which, happily enough, is numeric value rather similar to the figure we arrived at using Iain's equations, namely 304.4 KW. Only about 20 KW off. So far so good.
In the case of the second web-calculator, we seem to be even more "on the right track". The final value it gives once hub-gear inefficiency is deducted is 303.5 KW, almost identical to the value we obtained using Iain's equations, 304.4 KW:
Multiplying this figure by 1.43 hours, we get 434 KW for the duration.
**************************************************
13. Cañon City to Monarch Pass, at 90 kph with 18 kph headwind
**************************************************
Now let's calculate what happens when we add on another 18 kph for headwind to 90 kph, for a total air-velocity of 30 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (30 m/s)[SUP] 2[/SUP])/2 = 9868.5 m/s[SUP]2 [/SUP]divided by 2 = 4934.25 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 4,934.25 m/s[SUP]2[/SUP]= 12,468.35 kg m/s[SUP]2 [/SUP].
Multiplying this figure for FTotal by the TerraLiner's velocity of 25 m/s (the velocity without headwind), we get 311,708.75 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 311.7 KW per hour. We divide by 0.90 for hub-gear inefficiency and get 346.3 KW. Again travel time is 1.43 hours, or about 1 hour and 26 minutes, so our final figure is 346.3 KW x 1.43 = 495.3 KW.
**************************************************
IMPORTANT NOTE: throughout these calculations, in my final multiplication to get a power figure in Watts, I will be using the TerraLiner's velocity relative to the ground, and not its air-speed velocity. If I were to use the latter velocity, then I would be multiplying Froll and Fslope by the air-speed velocity, which seems just plain wrong. Perhaps a more accurate calculation would multiply Froll and Fslope by the TerraLiner's velocity relative to the gourd, and then a second calculation would multiple Fair by the airspeed velocity? That way one might get a more accurate representation of air-resistance as a cubic function, as v[SUP]3 [/SUP]. But Iain suggested simply multiplying the final sum of FTotal by the TerraLiner's velocity, so that's what I will be doing......
**************************************************
Now notice that when using Iain's equations, there is a 120 KW difference between the total or "absolute" amount of power required to climb this slope up to Monarch Pass at 50 kph with an 18 kph headwind (377.28 KW), versus the power required to climb the same slope at 90 kph with an 18 kph headwind (495.3 KW). Also notice the slightly non-linear progression. As we increased the airspeed from 68 kph to 90 kph, or 22 kph, the power consumption increased about 60 W. Now we are increasing the TerraLiner's airspeed just another 18 kph, and the power consumption jumps another 60 W. But the difference is not "dramatically" non-linear.
Again, before we jump to conclusions, let's use our web-calculators to confirm that we are roughly on the right track.
In the case of the first web-calculator, consulting the table that it produces we now look for values that are closest to 108 kph (i.e. 90 kph + 18 kph). Turns out there are values for 105 kph and 113 kph, so "averaging", we get a power figure for 108 kph of 241,228.67 W, or 241.2 KW:
"Averaging" is not perfect, because the increase in the values for power on this table are non-linear. But for my present purposes averaging will suffice.
Fslope is still the same, so all we need to do is add 122 KW + 241.2 KW, and we arrive at the per-hour consumption figure of 363.2 KW. This is only a bit different -- about 17 KW different -- than the power figure that we arrived at using Iain's equations, i.e. 346.3 KW per hour. In the previous comparison, the figure arrived at using the web-calculator was 20 KW less; in this case, 17 KW more. The difference could probably be accounted for by the fact that at the end of Iain's equations I only multiplied by 25 m/s, and not by 30 m/s, for the reason given. Whereas this web-calculator no doubt multiples Froll + Fair by 30 m/s, because it has no way of distinguishing between the speed of the TerraLiner relative to the air, versus the speed of the TerraLiner relative to the ground. So far so good.
In the case of the second web-calculator, however, our calculation using Iain's equations seems to be quite a bit more "off":
There is a big difference between 346.3 KW per hour, versus 414.4 KW per hour. But I think it can be explained, along with a few other anomalies that are cropping up.
The absolute power requirement figures produced by the second web-calculator, i.e the power requirements for a given distance, seem at first to be positively confusing. When the second web-calculator computed the power required per hour for 50 kph with an 18 kph headwind, it arrived at a figure of 198.4 KW. Multiplying this by a total travel time of 2.57 hours, we arrived at total figure for the duration of 505.09 KW -- again, see Section 7 in post #2108 at http://www.expeditionportal.com/for...w-6x6-Hybrid-Drivetrain?p=1973665#post1973665 . Now that the travel time is just 1.43 hours, our final figure for the duration at 90 kph with 18 kph headwind is 414.4 KW x 1.43 = 592.45 KW. If anything, this is an even more moderate jump than the 120 KW we arrived at using Iain's equations, a difference of just 87 KW.
However in between, for 90 kph without headwind, we got 434 KW for the duration, which is a lot less than than the power requirement for 50 kph + 18 kph. This makes no sense, until we think about what headwind actually represents. Headwind is like adding speed, which requires more power to overcome air-resistance, but without any of the benefit for the total power consumption for a given distance that comes from higher speed, i.e. the ability to cover more distance in less time.
Add to this the fact that to represent "50 kph + 18 kph headwind", I simply entered 68 kph into the second web-calculator. So when making the final multiplication by v, it will have multiplied Ftotal not by the TerraLiner's ground-speed, but rather, it will have multiplied Ftotal by the TerraLiner's airspeed. These two factors combined should account for the reason why 434 KW required at 90 kph is so much less than 505.08 KW required at 50 kph + headwind. It's then interesting for me that when we run parallel calculations for 90 kph straight, with no headwind, Iain's equations and this second web-calculator produce nearly the same result.
Once again, let's collect a few more data points before jumping to conclusions.....
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
14. 90 kph on a mountain highway? Colorado's I-70.
**************************************************
Here I simply want to note that 90 kph is of course unrealistic for this section of Route 50 in Colorado in particular. Google calculates the average speed along this stretch as 78.74 kph ("without traffic"), no doubt because this segment of Route 50 contains so many twists and turns. 90 kph would probably be impossible, even for a car; or otherwise very dangerous.
But a much wider and much more expensive, 4-lane mountain highway like the I-70 (which traverses the Eisenhower tunnel) could be driven more quickly. Google estimates 95 kph (i.e. 60 mph) as possible between Denver and the Eisenhower tunnel. Having driven the I-70 clear across Colorado in both directions, I can affirm that this is indeed possible, and then some.....:sombrero:...See https://en.wikipedia.org/wiki/Eisenhower_Tunnel , https://www.codot.gov/travel/eisenhower-tunnel/description.html , https://www.codot.gov/travel/eisenhower-tunnel , http://www.crashforensics.com/eisenhowerpass.cfm , https://www.google.co.uk/maps/dir/T...266aa577c950ef!2m2!1d-105.9056878!2d39.679042 :
Recall that the average grade on the I-70 between Denver and the Eisenhower tunnel is even steeper, 2.2 %, although the distance is shorter, just 46 miles or 74 km.
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
14. 90 kph on a mountain highway? Colorado's I-70.
**************************************************
Here I simply want to note that 90 kph is of course unrealistic for this section of Route 50 in Colorado in particular. Google calculates the average speed along this stretch as 78.74 kph ("without traffic"), no doubt because this segment of Route 50 contains so many twists and turns. 90 kph would probably be impossible, even for a car; or otherwise very dangerous.
But a much wider and much more expensive, 4-lane mountain highway like the I-70 (which traverses the Eisenhower tunnel) could be driven more quickly. Google estimates 95 kph (i.e. 60 mph) as possible between Denver and the Eisenhower tunnel. Having driven the I-70 clear across Colorado in both directions, I can affirm that this is indeed possible, and then some.....:sombrero:...See https://en.wikipedia.org/wiki/Eisenhower_Tunnel , https://www.codot.gov/travel/eisenhower-tunnel/description.html , https://www.codot.gov/travel/eisenhower-tunnel , http://www.crashforensics.com/eisenhowerpass.cfm , https://www.google.co.uk/maps/dir/T...266aa577c950ef!2m2!1d-105.9056878!2d39.679042 :
Recall that the average grade on the I-70 between Denver and the Eisenhower tunnel is even steeper, 2.2 %, although the distance is shorter, just 46 miles or 74 km.
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
Here are some maps that combine topography with highways, to provide some sense of how the I-70 cuts across the center of Colorado:
And here is a more detailed Google map of the I-70 between Denver and the Eisenhower tunnel:
The following is pretty much the only elevation-profile that I could find, but it's good enough for our purposes -- see http://www.mynissanleaf.com/viewtopic.php?t=14282 . It shows how the I-70 starts at roughly 5,210 feet in Denver (the altitude of Denver varies from 5,130 - 5,690 feet -- see https://en.wikipedia.org/wiki/Denver ), and tops out at 11,158 feet at the Eisenhower Tunnel (again, see https://en.wikipedia.org/wiki/Eisenhower_Tunnel ). The wonderful thing about this elevation profile is that it shows just how steep the I-70's slope becomes before and after the tunnel, as steep as 7 %:
Here are some videos of the Eisenhower Tunnel, and the I-70 leading up to it:
[video=youtube;uC70__BM_kw]https://www.youtube.com/watch?v=uC70__BM_kw [/video] [video=youtube;DLzvBQhBIS4]https://www.youtube.com/watch?v=DLzvBQhBIS4 [/video]
[video=youtube;6Y31Jw1RFdM]https://www.youtube.com/watch?v=6Y31Jw1RFdM [/video]
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
Here are some maps that combine topography with highways, to provide some sense of how the I-70 cuts across the center of Colorado:
And here is a more detailed Google map of the I-70 between Denver and the Eisenhower tunnel:
The following is pretty much the only elevation-profile that I could find, but it's good enough for our purposes -- see http://www.mynissanleaf.com/viewtopic.php?t=14282 . It shows how the I-70 starts at roughly 5,210 feet in Denver (the altitude of Denver varies from 5,130 - 5,690 feet -- see https://en.wikipedia.org/wiki/Denver ), and tops out at 11,158 feet at the Eisenhower Tunnel (again, see https://en.wikipedia.org/wiki/Eisenhower_Tunnel ). The wonderful thing about this elevation profile is that it shows just how steep the I-70's slope becomes before and after the tunnel, as steep as 7 %:
Here are some videos of the Eisenhower Tunnel, and the I-70 leading up to it:
[video=youtube;uC70__BM_kw]https://www.youtube.com/watch?v=uC70__BM_kw [/video] [video=youtube;DLzvBQhBIS4]https://www.youtube.com/watch?v=DLzvBQhBIS4 [/video]
[video=youtube;6Y31Jw1RFdM]https://www.youtube.com/watch?v=6Y31Jw1RFdM [/video]
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
[video=youtube;LNqcNH7ez4k]https://www.youtube.com/watch?v=LNqcNH7ez4k [/video] [video=youtube;vnEXuJYU7fQ]https://www.youtube.com/watch?v=vnEXuJYU7fQ [/video]
[video=youtube;8DIrsDsS80A]https://www.youtube.com/watch?v=8DIrsDsS80A [/video] [video=youtube;QecO-jNGV2Y]https://www.youtube.com/watch?v=QecO-jNGV2Y [/video] [video=youtube;haouuwMGJd4]https://www.youtube.com/watch?v=haouuwMGJd4 [/video]
The last four videos in particular capture how I remember driving this highway when I was still a young, irresponsible, and very impatient 20-something speed freak, with more testosterone than sense......:sombrero:
Now there is no question that some countries like Germany limit trucks to 90 kph, and buses to 100 kph -- see for instance https://en.wikipedia.org/wiki/Speed_limits_in_Germany. But Germany is not the world, and some countries allow trucks to drive as fast as 110 kph -- see https://en.wikipedia.org/wiki/Speed_limits_by_country . Within the United States, speed limits are the jurisdiction of states, and vary considerably -- see https://en.wikipedia.org/wiki/Speed_limits_in_the_United_States :
In fact, in Colorado in particular the speed for trucks on Interstate highways is 65 - 75 mph, or 105 - 120 kph. And on the I-70 in particular, it's 120 kph. So there does exist an ascent that's a 4-lane highway, where the TerraLiner could conceivably drive from Denver up to the Eisenhower tunnel at 120 kph. More about this in a later post.
I merely wanted to state all of this, simply to suggest that it's not a completely futile exercise to run calculations for 100 kph and above. Although I could not find equivalent speed-limit maps for trucks, let's just say that east-coast-American and/or British "intuitions" about what a reasonable speed limit should be, are not universally shared. Most of the world allows 75 or 80 mph for cars. And even in the United States, western mountain states are far more "speed sympathetic" than East Coast states or Britain. Permitted truck and bus speeds do not necessarily correlate with car speeds, however. For instance, Germany has no speed limit for cars on autobahns, but it does limit both trucks and buses.
It also needs to be added that if the TerraLiner wanted to do 100 kph and above on any highway, it would be a highway that was climbing. That way braking would be much easier, when necessary. There's also the business of "passing" a slow vehicle, say one that's doing 85 kph. But granted, the brief extra speed and power needed for passing would be provided by the batteries and electric hub motors, and this is not the same thing as maintaining a constant speed of 100 kph.
Finally, and perhaps most importantly, we need to develop a clearer picture of how increasing air-resistance at higher speeds will -- and will not -- have an impact on TerraLiner power efficiency. Put simply, we need to collect more data points in any case. More data points will also allow us to make further comparisons between the results obtained using Ian's equations, and the results produced by the on-line web-calcuators. So even though speeds of 100 kph and above may seem like unrealistic for some thread participants, one of my central motivations in the next few posts is purely mathematical. I want to see to what extent Iain's equations seem to "track" the results produced by the web-calculators, and/or to what extent either those results -- or Iain's equations -- might be a bit "off."
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
[video=youtube;LNqcNH7ez4k]https://www.youtube.com/watch?v=LNqcNH7ez4k [/video] [video=youtube;vnEXuJYU7fQ]https://www.youtube.com/watch?v=vnEXuJYU7fQ [/video]
[video=youtube;8DIrsDsS80A]https://www.youtube.com/watch?v=8DIrsDsS80A [/video] [video=youtube;QecO-jNGV2Y]https://www.youtube.com/watch?v=QecO-jNGV2Y [/video] [video=youtube;haouuwMGJd4]https://www.youtube.com/watch?v=haouuwMGJd4 [/video]
The last four videos in particular capture how I remember driving this highway when I was still a young, irresponsible, and very impatient 20-something speed freak, with more testosterone than sense......:sombrero:
Now there is no question that some countries like Germany limit trucks to 90 kph, and buses to 100 kph -- see for instance https://en.wikipedia.org/wiki/Speed_limits_in_Germany. But Germany is not the world, and some countries allow trucks to drive as fast as 110 kph -- see https://en.wikipedia.org/wiki/Speed_limits_by_country . Within the United States, speed limits are the jurisdiction of states, and vary considerably -- see https://en.wikipedia.org/wiki/Speed_limits_in_the_United_States :
In fact, in Colorado in particular the speed for trucks on Interstate highways is 65 - 75 mph, or 105 - 120 kph. And on the I-70 in particular, it's 120 kph. So there does exist an ascent that's a 4-lane highway, where the TerraLiner could conceivably drive from Denver up to the Eisenhower tunnel at 120 kph. More about this in a later post.
I merely wanted to state all of this, simply to suggest that it's not a completely futile exercise to run calculations for 100 kph and above. Although I could not find equivalent speed-limit maps for trucks, let's just say that east-coast-American and/or British "intuitions" about what a reasonable speed limit should be, are not universally shared. Most of the world allows 75 or 80 mph for cars. And even in the United States, western mountain states are far more "speed sympathetic" than East Coast states or Britain. Permitted truck and bus speeds do not necessarily correlate with car speeds, however. For instance, Germany has no speed limit for cars on autobahns, but it does limit both trucks and buses.
It also needs to be added that if the TerraLiner wanted to do 100 kph and above on any highway, it would be a highway that was climbing. That way braking would be much easier, when necessary. There's also the business of "passing" a slow vehicle, say one that's doing 85 kph. But granted, the brief extra speed and power needed for passing would be provided by the batteries and electric hub motors, and this is not the same thing as maintaining a constant speed of 100 kph.
Finally, and perhaps most importantly, we need to develop a clearer picture of how increasing air-resistance at higher speeds will -- and will not -- have an impact on TerraLiner power efficiency. Put simply, we need to collect more data points in any case. More data points will also allow us to make further comparisons between the results obtained using Ian's equations, and the results produced by the on-line web-calcuators. So even though speeds of 100 kph and above may seem like unrealistic for some thread participants, one of my central motivations in the next few posts is purely mathematical. I want to see to what extent Iain's equations seem to "track" the results produced by the web-calculators, and/or to what extent either those results -- or Iain's equations -- might be a bit "off."
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
15. Cañon City to Monarch Pass at 100 kph, without headwind
**************************************************
So first, here are the calculations for 100 kph, with no headwind. The distance is still Cañon City to Monarch Pass, or 128.6 km, the slope is still 1.4 %, and so only the third equation for Fair will change, because the air-velocity becomes 27.8 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (27.8 m/s)[SUP] 2[/SUP])/2 = 8474.19 m/s[SUP]2 [/SUP]divided by 2 = 4237.09 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 4237.09 m/s[SUP]2[/SUP]= 11,771.19 kg m/s[SUP]2 [/SUP].
Multiplying the second figure for FTotal by the TerraLiner's velocity of 27.8 m/s, we get 327,239.23 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 327.2 KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 363.6 KW. The TerraLiner is now traveling at 100 kph instead of 90 kph or 50 kph, so the travel time will be shorter, 1.286 hours, or about 1 hour and 17 minutes. Multiplying, we get 363.6 KW x 1.286 = 467.6 KW.
This is about 30 KW more than the total power figure for the duration of 25 m/s (90 kph) without a headwind, i.e. 435.4 KW. See Section 12 in post #2111 above, at http://www.expeditionportal.com/for...w-6x6-Hybrid-Drivetrain?p=1973703#post1973703 . But then we are not adding that much speed, just 10 kph, or 2.8 m/s. The next "jump" in the power requirement would be moving from 100 kph without headwind to 90 kph with an 18 kph headwind (108 kph in total), which as we already saw would require 495.3 KW. This represents another jump of almost 30 KW over 467.6 KW. After 495.3 KW there's a jump to 100 kph with headwind (118 kph in total), where the ultimate power figure will be 533.6 KW. That's another jump to be sure, this time almost 40 KW, but not exactly what one might call a radically non-linear "x[SUP]3[/SUP]" sort of jump. Or at the very least, we still seem to be in the low-increasing slope range of the v[SUP]3 [/SUP]function.....:sombrero:
Actually, I think that something else is going on, other than a cubic increase, especially when we calculate for the final power requirements for a given distance.
Double-checking using our web-calculators, for the first web-calculator we consult the table of figures, now looking for values closest to 100 kph, which would appear to be 97 kph and 105 kph. "Averaging", we get a power figure for 100 kph of 203,638.06 W, or 203.6 KW:
All we need to do now is add the power requirement for Fslope as calculated using Iain's equation. For a 1.4 % grade this was 4,394.9 kg m/s[SUP]2[/SUP]. Multiplying by our increased ground-speed velocity of 27.8 m/s (100 kph), we get 122,178.22 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 122.2 KW. Dividing by 0.9 for hub-gear inefficiency, we get 135.75 KW per hour. We then add this to the web-calculator's figure for Froll + Fslope (this figure already includes a discount for hub-gear inefficiency), and we arrive at the per-hour consumption figure of 203.6 KW + 135.75 KW = 339.35 KW. Again, this is a numeric value less than the one we just arrived at using Iain's equations, namely 363.6 KW. This time, about 24 KW less.
It's interesting that when we don't have headwind, the first web-calcuator arrives at a value that's less than Iain's equations; and when we do have headwind, it arrives at a value that is more, but only a bit more.....
In the case of the second web-calculator, however, we are once again very much on the right track. The final value it gives after hub-gear inefficiency is deducted is 362 KW, almost exactly the same result as we obtained using Iain's equations:
And again, multiplying this figure by 1.286 hours, or about 1 hour and 17 minutes, we get 465.5 KW for the duration.
**************************************************
16. Cañon City to Monarch Pass, at 100 kph with an 18 kph headwind
**************************************************
The distance is still Cañon City to Monarch Pass, or 128.6 km, the slope is still 1.4 %, and so only the third equation for Fair will change, because the air-velocity becomes 32.8 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (32.8 m/s)[SUP] 2[/SUP])/2 = 11,796.59 m/s[SUP]2 [/SUP]divided by 2 = 5898.29 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 5898.29 m/s[SUP]2[/SUP]= 13,432.39 kg m/s[SUP]2 [/SUP].
Multiplying the second figure for FTotal by the TerraLiner's ground-speed of 27.8 m/s (100 kph, without the headwind), we get 373,420.52 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 373.4 KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 414.9 KW. The TerraLiner is now traveling at 100 kph instead of 90 kph or 50 kph, so the travel time will be shorter, 1.286 hours. Multiplying, we get 414.9 KW x 1.286 = 533.6 KW.
Checking against the first web-calculator, we now look for values that are closest to 118 kph (i.e. 100 kph + 18 kph). Turns out there are values for 113 kph and 121 kph, so "averaging", we get a power figure for 118 kph of 295,178.20 W, or 295.2 KW:
Fslope is still the same and our ground-speed velocity is still the same, so all we need to do is add 135.75 KW + 295.2 KW, and we arrive at the per-hour consumption figure of 430.95 KW. Again, this is now more than the value that we got using Iain's equations, i.e. 414.9 KW per hour; about 16 KW more. Recall that in our previous calculation for 90 kph + a headwind of 18 kph , the first web-calculator's result diverged by 17 KW from Iain's equations, i.e. by 17 KW more.
But in the case of the second web-calculator, once again we get a figure that is considerably different from the one produced by Iain's equations, i.e we get 487.6 KW versus 414.9 KW per hour. And again, the difference is probably attributable to the reason already given above, i.e. the fact that using Iain's equations we only multiply Ftotal by the ground speed of 100 kph, and not by the air-speed of 118 kph:
The absolute power requirement figure produced by the second web-calculator, i.e the power requirements for a given distance, is then 1.286 hours x 487.6 KW = 627.05 KW for the duration. I find it interesting that this absolute power figure for the distance of 128.6 km, driven at 100 kph with an 18 kph headwind, is only about 35 KW more than the final figure given by the second web-calculator for the same distance driven at 90 kph with an 18 kph headwind, which we calculated as 592.45 KW.
I am now feeling strongly inclined to just dismiss the results of the second web-calculator for "headwind" as simply worthless, because it really has no way of distinguishing between 118 kph, versus 100 kph + 18 kph with headwind. It does not allow us to separate ground-speed from air-speed, in the way that Iain's equations enable us to do. The mere fact that when we run Iain's equations without headwind, we arrive at results that are almost exactly the same as the results produced by the second web-calculator, suggests to me that Iain's equations are very much "on track". We only arrive at a discrepancy when we try to pretend that the second web-calculator can do something that it was not designed to do, namely, calculate the power consumption for a given ground velocity + headwind.
So let's continue with a few more data points.....
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
15. Cañon City to Monarch Pass at 100 kph, without headwind
**************************************************
So first, here are the calculations for 100 kph, with no headwind. The distance is still Cañon City to Monarch Pass, or 128.6 km, the slope is still 1.4 %, and so only the third equation for Fair will change, because the air-velocity becomes 27.8 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (27.8 m/s)[SUP] 2[/SUP])/2 = 8474.19 m/s[SUP]2 [/SUP]divided by 2 = 4237.09 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 4237.09 m/s[SUP]2[/SUP]= 11,771.19 kg m/s[SUP]2 [/SUP].
Multiplying the second figure for FTotal by the TerraLiner's velocity of 27.8 m/s, we get 327,239.23 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 327.2 KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 363.6 KW. The TerraLiner is now traveling at 100 kph instead of 90 kph or 50 kph, so the travel time will be shorter, 1.286 hours, or about 1 hour and 17 minutes. Multiplying, we get 363.6 KW x 1.286 = 467.6 KW.
This is about 30 KW more than the total power figure for the duration of 25 m/s (90 kph) without a headwind, i.e. 435.4 KW. See Section 12 in post #2111 above, at http://www.expeditionportal.com/for...w-6x6-Hybrid-Drivetrain?p=1973703#post1973703 . But then we are not adding that much speed, just 10 kph, or 2.8 m/s. The next "jump" in the power requirement would be moving from 100 kph without headwind to 90 kph with an 18 kph headwind (108 kph in total), which as we already saw would require 495.3 KW. This represents another jump of almost 30 KW over 467.6 KW. After 495.3 KW there's a jump to 100 kph with headwind (118 kph in total), where the ultimate power figure will be 533.6 KW. That's another jump to be sure, this time almost 40 KW, but not exactly what one might call a radically non-linear "x[SUP]3[/SUP]" sort of jump. Or at the very least, we still seem to be in the low-increasing slope range of the v[SUP]3 [/SUP]function.....:sombrero:
Actually, I think that something else is going on, other than a cubic increase, especially when we calculate for the final power requirements for a given distance.
Double-checking using our web-calculators, for the first web-calculator we consult the table of figures, now looking for values closest to 100 kph, which would appear to be 97 kph and 105 kph. "Averaging", we get a power figure for 100 kph of 203,638.06 W, or 203.6 KW:
All we need to do now is add the power requirement for Fslope as calculated using Iain's equation. For a 1.4 % grade this was 4,394.9 kg m/s[SUP]2[/SUP]. Multiplying by our increased ground-speed velocity of 27.8 m/s (100 kph), we get 122,178.22 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 122.2 KW. Dividing by 0.9 for hub-gear inefficiency, we get 135.75 KW per hour. We then add this to the web-calculator's figure for Froll + Fslope (this figure already includes a discount for hub-gear inefficiency), and we arrive at the per-hour consumption figure of 203.6 KW + 135.75 KW = 339.35 KW. Again, this is a numeric value less than the one we just arrived at using Iain's equations, namely 363.6 KW. This time, about 24 KW less.
It's interesting that when we don't have headwind, the first web-calcuator arrives at a value that's less than Iain's equations; and when we do have headwind, it arrives at a value that is more, but only a bit more.....
In the case of the second web-calculator, however, we are once again very much on the right track. The final value it gives after hub-gear inefficiency is deducted is 362 KW, almost exactly the same result as we obtained using Iain's equations:
And again, multiplying this figure by 1.286 hours, or about 1 hour and 17 minutes, we get 465.5 KW for the duration.
**************************************************
16. Cañon City to Monarch Pass, at 100 kph with an 18 kph headwind
**************************************************
The distance is still Cañon City to Monarch Pass, or 128.6 km, the slope is still 1.4 %, and so only the third equation for Fair will change, because the air-velocity becomes 32.8 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (32.8 m/s)[SUP] 2[/SUP])/2 = 11,796.59 m/s[SUP]2 [/SUP]divided by 2 = 5898.29 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 5898.29 m/s[SUP]2[/SUP]= 13,432.39 kg m/s[SUP]2 [/SUP].
Multiplying the second figure for FTotal by the TerraLiner's ground-speed of 27.8 m/s (100 kph, without the headwind), we get 373,420.52 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 373.4 KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 414.9 KW. The TerraLiner is now traveling at 100 kph instead of 90 kph or 50 kph, so the travel time will be shorter, 1.286 hours. Multiplying, we get 414.9 KW x 1.286 = 533.6 KW.
Checking against the first web-calculator, we now look for values that are closest to 118 kph (i.e. 100 kph + 18 kph). Turns out there are values for 113 kph and 121 kph, so "averaging", we get a power figure for 118 kph of 295,178.20 W, or 295.2 KW:
Fslope is still the same and our ground-speed velocity is still the same, so all we need to do is add 135.75 KW + 295.2 KW, and we arrive at the per-hour consumption figure of 430.95 KW. Again, this is now more than the value that we got using Iain's equations, i.e. 414.9 KW per hour; about 16 KW more. Recall that in our previous calculation for 90 kph + a headwind of 18 kph , the first web-calculator's result diverged by 17 KW from Iain's equations, i.e. by 17 KW more.
But in the case of the second web-calculator, once again we get a figure that is considerably different from the one produced by Iain's equations, i.e we get 487.6 KW versus 414.9 KW per hour. And again, the difference is probably attributable to the reason already given above, i.e. the fact that using Iain's equations we only multiply Ftotal by the ground speed of 100 kph, and not by the air-speed of 118 kph:
The absolute power requirement figure produced by the second web-calculator, i.e the power requirements for a given distance, is then 1.286 hours x 487.6 KW = 627.05 KW for the duration. I find it interesting that this absolute power figure for the distance of 128.6 km, driven at 100 kph with an 18 kph headwind, is only about 35 KW more than the final figure given by the second web-calculator for the same distance driven at 90 kph with an 18 kph headwind, which we calculated as 592.45 KW.
I am now feeling strongly inclined to just dismiss the results of the second web-calculator for "headwind" as simply worthless, because it really has no way of distinguishing between 118 kph, versus 100 kph + 18 kph with headwind. It does not allow us to separate ground-speed from air-speed, in the way that Iain's equations enable us to do. The mere fact that when we run Iain's equations without headwind, we arrive at results that are almost exactly the same as the results produced by the second web-calculator, suggests to me that Iain's equations are very much "on track". We only arrive at a discrepancy when we try to pretend that the second web-calculator can do something that it was not designed to do, namely, calculate the power consumption for a given ground velocity + headwind.
So let's continue with a few more data points.....
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
17. Cañon City to Monarch Pass at 110 kph, without headwind
**************************************************
Here are the calculations for 110 kph, with no headwind. The distance is still Cañon City to Monarch Pass, 128.6 km, the slope is still 1.4 %, and only the value for Fair will change, because the air-velocity (the same as the ground velocity) becomes 30.56 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (30.56 m/s)[SUP] 2 [/SUP])/2 = 10,240.36 m/s[SUP]2 [/SUP]divided by 2 = 5,120.18 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 5,120.18 m/s[SUP]2[/SUP]= 12,654.28 kg m/s[SUP]2 [/SUP].
Multiplying the second figure for FTotal by the TerraLiner's ground velocity of 30.56 m/s, we get 386,714.80 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 386.7 KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 429.67 KW. The TerraLiner is now traveling at 110 kph instead of 100 kph, so the travel time required to cover 128.6 km will be shorter, 1.169 hours, or about 1 hour and 10 minutes. Multiplying, we get 429.67 KW x 1.169 = 502.28 KW.
This is about 35 KW more than the total power figure for the duration of 27.8 m/s (100 kph) without a headwind, i.e. 467.6 KW. See section 15 in the previous post. But again, we are not adding that much speed, just 10 kph, or 2.8 m/s.
Double-checking using our web-calculators, for the first web-calculator we consult the table of figures, now looking for values closest to 110 kph, which would appear to be 105 kph and 113 kph. "Averaging", we get a power figure for 110 kph of 251,374.19 W, or 251.4 KW:
Next, we add the power requirement for Fslope as calculated using Iain's equation, which for a 1.4 % grade is still 4,394.9 kg m/s[SUP]2[/SUP]. Multiplying by 30.56 m/s (110 kph), we get 134,308.14 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 134.3 KW. Dividing by 0.9 for hub-gear inefficiency, we get 149 KW per hour. We then add this to the web-calculator's figure for Froll + Fslope (this figure already includes a discount for hub-gear inefficiency), and we arrive at the per-hour consumption figure of 251.4 KW + 149 KW = 400.4 KW. Here again, without headwind, the first web-calculator produces a result slightly less than Iain's equations. Iain's equations produced 429.67 KW, and this web-calculator produced about 30 KW less, 400.4 KW.
In the case of the second web-calculator, predictably enough we get a nearly identical result, 428.37 KW:
And again, multiplying this figure by 1.169 hours, or about 1 hour and 10 minutes, we get 500.76 KW for the duration.
**************************************************
18. Cañon City to Monarch Pass, at 110 kph with an 18 kph headwind
**************************************************
The distance is 128.6 km, the slope is still 1.4 %, and so only the third equation for Fair will change, because the air-velocity becomes 110 kph + 18 kph = 128 kph = 35.56 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (35.56 m/s)[SUP] 2[/SUP])/2 = 13,865.39 m/s[SUP]2 [/SUP]divided by 2 = 6932.70 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 6932.70 m/s[SUP]2[/SUP]= 14,466.80 kg m/s[SUP]2 [/SUP].
Multiplying the second figure for FTotal by the TerraLiner's ground-speed of 30.56 (110 kph, without the headwind), we get 442,105.41 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 442.1 KWper hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 491.2 KW. The TerraLiner is now traveling at 110 kph instead of 100 kph, so the travel time is 1.169 hours; multiplying, we get 491.2 KW x 1.169 = 574.21 KW.
Checking against the first web-calculator, we now look for values that are closest to 128 kph (i.e. 110 kph + 18 kph). Turns out that there is a value for 129 kph, so "averaging" down to 128 kph, we get a power figure for 128 kph of 357,182.21 W, or 357.18 KW:
Fslope is still the same and our ground-speed velocity is still the same (110 kph), so all we need to do is add 149 KW + 357.18 KW, and we arrive at the per-hour consumption figure of 506.18KW. Again, this is now more than the value that we got using Iain's equations, i.e. 491.2 KW per hour; about 15 KW more. Recall that in our previous calculations including a headwind, this first web-calculator diverged by 17 KW and 16 KW more than Iain's equations.
In the case of the second web-calculator once again we get a figure that differs considerably different from the one produced by Iain's equations, i.e we get 570.01KW versus 491.2 KW per hour (again, see http://buggies.builtforfun.co.uk/Calculator/index.html and http://buggies.builtforfun.co.uk/Calculator/analyse-metric.php ):
Although 570.01KW would be an accurate value for the TerraLiner traveling up this slope with a ground-speed of 128 kph, and no headwind, it is not an accurate figure for 110 kph with an 18 kph headwind. This second web-calculator will have multiplied Ftotal by the air-speed of 128 kph, and not merely by the ground-speed of 110 kph, as per Iain's equations.
Be that as it may, the absolute power requirement figure produced by this second web-calculator, i.e the power requirements for a given distance, is then 1.169 hours x 570.01 KW = 666.34 KW. for the duration. Again, I find it interesting that this absolute power figure for the distance of 128.6 km, driven at 110 kph with an 18 kph headwind, is only about 39 KW more than the final figure given by the second web-calculator for the same distance driven at 100 kph with an 18 kph headwind, which we calculated as 627.05 KW.
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
17. Cañon City to Monarch Pass at 110 kph, without headwind
**************************************************
Here are the calculations for 110 kph, with no headwind. The distance is still Cañon City to Monarch Pass, 128.6 km, the slope is still 1.4 %, and only the value for Fair will change, because the air-velocity (the same as the ground velocity) becomes 30.56 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (30.56 m/s)[SUP] 2 [/SUP])/2 = 10,240.36 m/s[SUP]2 [/SUP]divided by 2 = 5,120.18 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 5,120.18 m/s[SUP]2[/SUP]= 12,654.28 kg m/s[SUP]2 [/SUP].
Multiplying the second figure for FTotal by the TerraLiner's ground velocity of 30.56 m/s, we get 386,714.80 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 386.7 KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 429.67 KW. The TerraLiner is now traveling at 110 kph instead of 100 kph, so the travel time required to cover 128.6 km will be shorter, 1.169 hours, or about 1 hour and 10 minutes. Multiplying, we get 429.67 KW x 1.169 = 502.28 KW.
This is about 35 KW more than the total power figure for the duration of 27.8 m/s (100 kph) without a headwind, i.e. 467.6 KW. See section 15 in the previous post. But again, we are not adding that much speed, just 10 kph, or 2.8 m/s.
Double-checking using our web-calculators, for the first web-calculator we consult the table of figures, now looking for values closest to 110 kph, which would appear to be 105 kph and 113 kph. "Averaging", we get a power figure for 110 kph of 251,374.19 W, or 251.4 KW:
Next, we add the power requirement for Fslope as calculated using Iain's equation, which for a 1.4 % grade is still 4,394.9 kg m/s[SUP]2[/SUP]. Multiplying by 30.56 m/s (110 kph), we get 134,308.14 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 134.3 KW. Dividing by 0.9 for hub-gear inefficiency, we get 149 KW per hour. We then add this to the web-calculator's figure for Froll + Fslope (this figure already includes a discount for hub-gear inefficiency), and we arrive at the per-hour consumption figure of 251.4 KW + 149 KW = 400.4 KW. Here again, without headwind, the first web-calculator produces a result slightly less than Iain's equations. Iain's equations produced 429.67 KW, and this web-calculator produced about 30 KW less, 400.4 KW.
In the case of the second web-calculator, predictably enough we get a nearly identical result, 428.37 KW:
And again, multiplying this figure by 1.169 hours, or about 1 hour and 10 minutes, we get 500.76 KW for the duration.
**************************************************
18. Cañon City to Monarch Pass, at 110 kph with an 18 kph headwind
**************************************************
The distance is 128.6 km, the slope is still 1.4 %, and so only the third equation for Fair will change, because the air-velocity becomes 110 kph + 18 kph = 128 kph = 35.56 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (35.56 m/s)[SUP] 2[/SUP])/2 = 13,865.39 m/s[SUP]2 [/SUP]divided by 2 = 6932.70 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 6932.70 m/s[SUP]2[/SUP]= 14,466.80 kg m/s[SUP]2 [/SUP].
Multiplying the second figure for FTotal by the TerraLiner's ground-speed of 30.56 (110 kph, without the headwind), we get 442,105.41 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 442.1 KWper hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 491.2 KW. The TerraLiner is now traveling at 110 kph instead of 100 kph, so the travel time is 1.169 hours; multiplying, we get 491.2 KW x 1.169 = 574.21 KW.
Checking against the first web-calculator, we now look for values that are closest to 128 kph (i.e. 110 kph + 18 kph). Turns out that there is a value for 129 kph, so "averaging" down to 128 kph, we get a power figure for 128 kph of 357,182.21 W, or 357.18 KW:
Fslope is still the same and our ground-speed velocity is still the same (110 kph), so all we need to do is add 149 KW + 357.18 KW, and we arrive at the per-hour consumption figure of 506.18KW. Again, this is now more than the value that we got using Iain's equations, i.e. 491.2 KW per hour; about 15 KW more. Recall that in our previous calculations including a headwind, this first web-calculator diverged by 17 KW and 16 KW more than Iain's equations.
In the case of the second web-calculator once again we get a figure that differs considerably different from the one produced by Iain's equations, i.e we get 570.01KW versus 491.2 KW per hour (again, see http://buggies.builtforfun.co.uk/Calculator/index.html and http://buggies.builtforfun.co.uk/Calculator/analyse-metric.php ):
Although 570.01KW would be an accurate value for the TerraLiner traveling up this slope with a ground-speed of 128 kph, and no headwind, it is not an accurate figure for 110 kph with an 18 kph headwind. This second web-calculator will have multiplied Ftotal by the air-speed of 128 kph, and not merely by the ground-speed of 110 kph, as per Iain's equations.
Be that as it may, the absolute power requirement figure produced by this second web-calculator, i.e the power requirements for a given distance, is then 1.169 hours x 570.01 KW = 666.34 KW. for the duration. Again, I find it interesting that this absolute power figure for the distance of 128.6 km, driven at 110 kph with an 18 kph headwind, is only about 39 KW more than the final figure given by the second web-calculator for the same distance driven at 100 kph with an 18 kph headwind, which we calculated as 627.05 KW.
**************************************************
CONTINUED IN NEXT POST
.
Last edited:
biotect
Designer
.
CONTINUED FROM PREVIOUS POST
**************************************************
19. Cañon City to Monarch Pass at 120 kph, without headwind
**************************************************
To round things out, lets do calculations for both 120 kph and 50 kph without a headwind. If the above pattern holds then when checking figures obtained using Iain's equations against our two web-calculators, the first should produce results slightly lower than Iain's equations, while the second should produce results are almost exactly the same as Iain's equations.
The distance is still Cañon City to Monarch Pass, 128.6 km, the slope is still 1.4 %, and only the value for Fair will change, because the air-velocity (the same as the ground velocity) becomes 120 kph, or 33.33 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (33.33 m/s)[SUP]2 [/SUP])/2 = 12,180.90 m/s[SUP]2 [/SUP]divided by 2 = 6090.45 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 6090.45 m/s[SUP]2[/SUP]= 13,624.55 kg m/s[SUP]2 [/SUP]
Multiplying the second figure for FTotal by the TerraLiner's ground velocity of 33.33 m/s, we get 454,106.20 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 454.1 KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 504.56 KW per hour. The TerraLiner is now traveling at 120 kph instead of 110 kph, so the travel time required to cover 128.6 km will be shorter, 1.0717 hours, or about 1 hour and 4 minutes. Multiplying, we get 429.67 KW x 1.169 = 540.74 KW in total for the duration.
This is about 38 KW more than the total power figure that we calculated for the duration at 30.56 m/s (110 kph) without a headwind, i.e. 502.28 KW. Recall that the previous jumps were 35 KW and 30 KW, so the power consumption for a given distance is rising faster than the speed, but not dramatically so.
Double-checking using our web-calculators, for the first web-calculator we consult the table of figures, now looking for values closest to 120 kph, which would appear to be 121 kph. "Averaging", we get a power figure for 120 kph of 306,612.47 W, or 306.6 KW:
Next, we add the power requirement for Fslope as calculated using Iain's equation, which for a 1.4 % grade is still 4,394.9 kg m/s[SUP]2[/SUP]. Now multiplying by 33.33 m/s (120 kph), we get 146,482.02 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 146.48 KW. Dividing by 0.9 for hub-gear inefficiency, we get 162.76 KW per hour. We then add this to the web-calculator's figure for Froll + Fslope (this figure already includes a discount for hub-gear inefficiency), and we arrive at the per-hour consumption figure of 306.6 KW + 162.76 KW = 469.36 KW. Here again, without headwind, the first web-calculator produces a result slightly less than Iain's equations, about 33 KW less, 469.36 KW instead of 502.28 KW
In the case of the second web-calculator, predictably enough we get a nearly identical result to Iain's equations. Ian's equations produced 504.56 KW per hour, and this second web-calcualtor produces 503.35 KW:
Multiplying this figure by 1.0717 hours, we get 539.44 KW for the duration of the climb.
**************************************************
20. Cañon City to Monarch Pass at 50 kph, without headwind
**************************************************
Let's also go in the other direction, to see how the web-calculators compare relative to Iain's equations for a much lower value, 50 kph without a headwind.
The distance (128.6 km) and the slope (1.4 %) are still the same, only the value for Fair changes, and the air-velocity -- the same as the ground velocity -- is 50 kph, or 13.89 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (13.89 m/s)[SUP]2 [/SUP])/2 = 21,115.50 m/s[SUP]2 [/SUP]divided by 2 = 1,057.75 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 1,057.75 m/s[SUP]2[/SUP]= 8,591.85 kg m/s[SUP]2 [/SUP]. .1
Multiplying the second figure for FTotal by the TerraLiner's ground velocity of 13.89 m/s, we get 119,340.80 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 119.34 KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 132.60 KW per hour. The TerraLiner is now traveling at 50 kph instead of 120 kph, so the travel time required to cover 128.6 km will be much longer, 2.572 hours, or about 2 hour and 34 minutes. Multiplying, we get 132.60 KW x 2.572 hours = 341.05KW in total for the duration.
Double-checking using our web-calculators, for the first web-calculator we consult the table of figures, now looking for values closest to 50 kph, which would appear to be 48 kph and 56 kph. "Averaging", we get a power figure for 50 kph of 59,043.39 W, or 59 KW:
Next, we add the power requirement for Fslope as calculated using Iain's equation, which for a 1.4 % grade is still 4,394.9 kg m/s[SUP]2[/SUP]. Now multiplying by 13.89 m/s (50 kph), we get 61,045.16 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 61 KW. Dividing by 0.9 for hub-gear inefficiency, we get 67.8 KW per hour. We then add this to the web-calculator's figure for Froll + Fslope (this figure already includes a discount for hub-gear inefficiency), and we arrive at the per-hour consumption figure of 59 KW + 67.8 KW = 126.8 KW. Here again, without headwind, the first web-calculator produces a result slightly less than Iain's equations, about 6 KW less, 126.8 KWinstead of 132.60 KW per hour.
In the case of the second web-calculator, predictably enough we get a nearly identical result to Iain's equations. Ian's equations produced 132.60KW per hour, and this second web-calcualtor produces 132.04 KW, again, a nearly identical result:
Multiplying this figure by 2.572 hours, we get 339.61 KW for the duration of the climb.
**************************************************
CONTINUED IN NEXT POST
.
CONTINUED FROM PREVIOUS POST
**************************************************
19. Cañon City to Monarch Pass at 120 kph, without headwind
**************************************************
To round things out, lets do calculations for both 120 kph and 50 kph without a headwind. If the above pattern holds then when checking figures obtained using Iain's equations against our two web-calculators, the first should produce results slightly lower than Iain's equations, while the second should produce results are almost exactly the same as Iain's equations.
The distance is still Cañon City to Monarch Pass, 128.6 km, the slope is still 1.4 %, and only the value for Fair will change, because the air-velocity (the same as the ground velocity) becomes 120 kph, or 33.33 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (33.33 m/s)[SUP]2 [/SUP])/2 = 12,180.90 m/s[SUP]2 [/SUP]divided by 2 = 6090.45 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 6090.45 m/s[SUP]2[/SUP]= 13,624.55 kg m/s[SUP]2 [/SUP]
Multiplying the second figure for FTotal by the TerraLiner's ground velocity of 33.33 m/s, we get 454,106.20 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 454.1 KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 504.56 KW per hour. The TerraLiner is now traveling at 120 kph instead of 110 kph, so the travel time required to cover 128.6 km will be shorter, 1.0717 hours, or about 1 hour and 4 minutes. Multiplying, we get 429.67 KW x 1.169 = 540.74 KW in total for the duration.
This is about 38 KW more than the total power figure that we calculated for the duration at 30.56 m/s (110 kph) without a headwind, i.e. 502.28 KW. Recall that the previous jumps were 35 KW and 30 KW, so the power consumption for a given distance is rising faster than the speed, but not dramatically so.
Double-checking using our web-calculators, for the first web-calculator we consult the table of figures, now looking for values closest to 120 kph, which would appear to be 121 kph. "Averaging", we get a power figure for 120 kph of 306,612.47 W, or 306.6 KW:
Next, we add the power requirement for Fslope as calculated using Iain's equation, which for a 1.4 % grade is still 4,394.9 kg m/s[SUP]2[/SUP]. Now multiplying by 33.33 m/s (120 kph), we get 146,482.02 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 146.48 KW. Dividing by 0.9 for hub-gear inefficiency, we get 162.76 KW per hour. We then add this to the web-calculator's figure for Froll + Fslope (this figure already includes a discount for hub-gear inefficiency), and we arrive at the per-hour consumption figure of 306.6 KW + 162.76 KW = 469.36 KW. Here again, without headwind, the first web-calculator produces a result slightly less than Iain's equations, about 33 KW less, 469.36 KW instead of 502.28 KW
In the case of the second web-calculator, predictably enough we get a nearly identical result to Iain's equations. Ian's equations produced 504.56 KW per hour, and this second web-calcualtor produces 503.35 KW:
Multiplying this figure by 1.0717 hours, we get 539.44 KW for the duration of the climb.
**************************************************
20. Cañon City to Monarch Pass at 50 kph, without headwind
**************************************************
Let's also go in the other direction, to see how the web-calculators compare relative to Iain's equations for a much lower value, 50 kph without a headwind.
The distance (128.6 km) and the slope (1.4 %) are still the same, only the value for Fair changes, and the air-velocity -- the same as the ground velocity -- is 50 kph, or 13.89 m/s:
Fair = (1.29 kg/m³ x 0.85 x 10 m[SUP]2[/SUP] x (13.89 m/s)[SUP]2 [/SUP])/2 = 21,115.50 m/s[SUP]2 [/SUP]divided by 2 = 1,057.75 m/s[SUP]2[/SUP]
FTotal = 3139.2 kg m/s[SUP]2[/SUP] + 4,394.9 kg m/s[SUP]2 [/SUP]+ 1,057.75 m/s[SUP]2[/SUP]= 8,591.85 kg m/s[SUP]2 [/SUP]. .1
Multiplying the second figure for FTotal by the TerraLiner's ground velocity of 13.89 m/s, we get 119,340.80 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 119.34 KW per hour. We have to divide by 0.90 to account for hub-gear inefficiency, so we get 132.60 KW per hour. The TerraLiner is now traveling at 50 kph instead of 120 kph, so the travel time required to cover 128.6 km will be much longer, 2.572 hours, or about 2 hour and 34 minutes. Multiplying, we get 132.60 KW x 2.572 hours = 341.05KW in total for the duration.
Double-checking using our web-calculators, for the first web-calculator we consult the table of figures, now looking for values closest to 50 kph, which would appear to be 48 kph and 56 kph. "Averaging", we get a power figure for 50 kph of 59,043.39 W, or 59 KW:
Next, we add the power requirement for Fslope as calculated using Iain's equation, which for a 1.4 % grade is still 4,394.9 kg m/s[SUP]2[/SUP]. Now multiplying by 13.89 m/s (50 kph), we get 61,045.16 m[SUP]2[/SUP]/s[SUP]3[/SUP], or 61 KW. Dividing by 0.9 for hub-gear inefficiency, we get 67.8 KW per hour. We then add this to the web-calculator's figure for Froll + Fslope (this figure already includes a discount for hub-gear inefficiency), and we arrive at the per-hour consumption figure of 59 KW + 67.8 KW = 126.8 KW. Here again, without headwind, the first web-calculator produces a result slightly less than Iain's equations, about 6 KW less, 126.8 KWinstead of 132.60 KW per hour.
In the case of the second web-calculator, predictably enough we get a nearly identical result to Iain's equations. Ian's equations produced 132.60KW per hour, and this second web-calcualtor produces 132.04 KW, again, a nearly identical result:
Multiplying this figure by 2.572 hours, we get 339.61 KW for the duration of the climb.
**************************************************
CONTINUED IN NEXT POST
.
Last edited: